Question

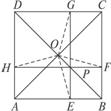
如图2-2-11,已知四边形ABCD内接于⊙O,AB是直径,AD =DC,分别延长BA、CD交于点E,BF⊥EC,交EC的延长线于F,若EA =AO,BC =12.求CF的长.

图2-2-11

Answer 1

思路分析:在Rt△CFB中,已知BC=12,要求CF,只有寻找与它相似的三角形,根据四边形ABCD内接于⊙O,则∠BCF =∠BAD,因此连结BD,构造Rt△BAD,下面证明△BAD∽△BCF.

解:连结OD、BD,?

∵AD = DC,∴AD =DC.?

∴∠ABC  m     m      m    ∠AOD.?

∴OD∥BC.∴=.?

∵EA =AO =BO,BC=12,?

∴OD =8.∴AB =16,EB =24.?

∵四边形ABCD内接于⊙O,?

∴∠EDA =∠EBC.∴△EDA∽△EBC.?

∴= =.?

设AD =CD =x,ED =y,?

则= =,解得, ,?

∴.?

∵AB为⊙O的直径,∴∠ADB =∠F =90°.?

又∠DAB =∠FCB,∴Rt△ADB∽Rt△CFB.?

∴=,即=,?

∴.