题目内容
如图2-2-11，已知P为正方形ABCD的对角线BD上的一点，通过P作正方形的边的垂线，垂足为E、F、G、H.你能判断出E、F、G、H是否在同一个圆上吗？试说明你的猜想.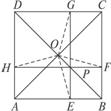
图2-2-11
思路分析:根据正方形的对称性，可以猜想，此四个点应当在以O为圆心的圆上，于是连结线段OE、OF、OG、OH，再设法证明这四条线段相等.
解:猜想：E、F、G、H四个点在以O为圆心的圆上.
证明:如图，连结线段OE、OF、OG、OH.在△OBE、△OBF、△OCG、△OAH中，OB=OC=OA.
∵PEBF为正方形，∴BE=BF=CG=AH，∠OBE=∠OBF=∠OCG=∠OAH.
∴△OBE≌△OBF≌△OCG≌△OAH.
∴OE=OF=OG=OH.
由圆的定义可知：E、F、G、H在以O为圆心的圆上.
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
