题目内容
【题目】已知椭圆![]() 的中点在原点,焦点在
的中点在原点,焦点在![]() 轴上,离心率
轴上,离心率![]() ,以两个焦点和短轴的两个端点为顶点的四边形的周长为8,面积为
,以两个焦点和短轴的两个端点为顶点的四边形的周长为8,面积为![]() .
.
(1)求椭圆![]() 的方程;
的方程;
(2)过原点![]() 的两条直线
的两条直线![]() ,
, ![]() ,交椭圆
,交椭圆![]() 于
于![]() ,
, ![]() ,
, ![]() ,
, ![]() 四点,若
四点,若![]() ,求四边形
,求四边形![]() 的面积.
的面积.
【答案】(1)![]() ;(2)
;(2)![]() .
.
【解析】试题分析:(1)依题意,根据椭圆的几何意义,求得![]() 的值,即可得到椭圆的方程;
的值,即可得到椭圆的方程;
(2)由题意设直线![]() 的方程与椭圆的方程联立方程组,得出
的方程与椭圆的方程联立方程组,得出![]() ,再由
,再由![]() ,求出
,求出![]() 的关系式,然后把四边形
的关系式,然后把四边形![]() 的面积转化为
的面积转化为![]() 的面积,结合
的面积,结合![]() 的关系式,代入便可得到结果.
的关系式,代入便可得到结果.
试题解析:
(1)依题意,设椭圆![]() 的方程为
的方程为![]() (
(![]() ),焦距为
),焦距为![]() ,
,
由题设条件可知, ![]() ,即
,即![]() ,
,
又![]() ,
, ![]() ,
,
解得![]() ,
, ![]() 或
或![]() ,
, ![]() (经检验不合题意,舍去).
(经检验不合题意,舍去).
故椭圆![]() 的方程为
的方程为![]() .
.
(2)不妨设![]() ,
, ![]() 位于
位于![]() 轴的上方,则直线
轴的上方,则直线![]() 的斜率一定存在,设直线
的斜率一定存在,设直线![]() 的方程为
的方程为![]() ,
, ![]() ,
, ![]() ,联立,得
,联立,得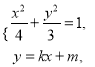 整理得
整理得![]() ,则
,则![]() ①,
①,![]() ②.
②.
由![]() 得,
得, ![]() ,将①②代入得
,将①②代入得![]() .
.
因为原点到直线![]() 的距离
的距离![]() ,
, 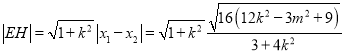 ,所以
,所以![]() ,
,
故四边形![]() 的面积为
的面积为![]() .
.

练习册系列答案
 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案 名题训练系列答案
名题训练系列答案
相关题目
【题目】某中学每年暑假举行“学科思维讲座”活动,每场讲座结束时,所有听讲这都要填写一份问卷调查.2017年暑假某一天五场讲座收到的问卷份数情况如下表:
学科 | 语文 | 数学 | 英语 | 理综 | 文综 |
问卷份数 |
|
|
|
|
|
用分层抽样的方法从这一天的所有问卷中抽取![]() 份进行统计,结果如下表:
份进行统计,结果如下表:
满意 | 一般 | 不满意 | |
语文 |
|
|
|
数学 |
| 1 |
|
英语 |
|
|
|
理综 |
|
|
|
文综 |
|
|
|
(1)估计这次讲座活动的总体满意率;
(2)求听数学讲座的甲某的调查问卷被选中的概率;
(3)若想从调查问卷被选中且填写不满意的人中再随机选出![]() 人进行家访,求这
人进行家访,求这![]() 人中选择的是理综讲座的人数的分布列.
人中选择的是理综讲座的人数的分布列.

