题目内容
18. 如图,在△ABC中,∠C=90°,∠ABC平分线BE交AC于点E,点D在AB上,∠DEB=90°.
如图,在△ABC中,∠C=90°,∠ABC平分线BE交AC于点E,点D在AB上,∠DEB=90°.(Ⅰ)求证:AC是△BDE的外接圆的切线;
(Ⅱ)若AD=2$\sqrt{3}$,AE=6,求△BDE的面积.
分析 (I)取BD的中点O,连接OE,通过证明OE⊥AC,可得AC是△BDE的外接圆的切线.
(II)利用射影定理AE2=AD•AB,求出AB,推出∠DBE=30°,求出BE=6,然后求解三角形的面积.
解答 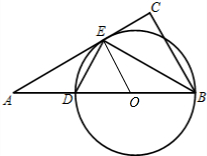 解:(I)取BD的中点O,连接OE,∵BE平分∠ABC,∴∠CBE=∠OBE,
解:(I)取BD的中点O,连接OE,∵BE平分∠ABC,∴∠CBE=∠OBE,
又∵OB=OE,∴∠OBE=∠BEO,∴∠CBE=∠BEO,∴BC∥OE,
∵∠C=90°,∴OE⊥AC,∴AC是△BDE的外接圆的切线;…(5分)
(II)∵$AD=2\sqrt{3}$,AE=6,AE2=AD•AB,
∴$AB=6\sqrt{3}$,∴$OE=\frac{1}{2}DB=2\sqrt{3}=\frac{1}{2}AO$,
∴∠A=30°,∴∠DBE=30°,∴$DE=2\sqrt{3}$,BE=6,
∴△BDE的面积是$6\sqrt{3}$.…(10分)
点评 本题考查圆的切线的证明,三角形的面积的求法,考查逻辑推理能力以及计算能力.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
7.已知i为虚数单位,若复数z满足(z-2i)(2-i)=5,则z的虚部等于( )
| A. | 2 | B. | 3 | C. | 2i | D. | 3i |
13. 定义一种运算符号“→”,两个实数a,b的“a→b”运算原理如图所示,若f(x)=(0→x)•x-(2→x),则y=f(x)在x∈[-2,2]时的最小值是( )
定义一种运算符号“→”,两个实数a,b的“a→b”运算原理如图所示,若f(x)=(0→x)•x-(2→x),则y=f(x)在x∈[-2,2]时的最小值是( )
 定义一种运算符号“→”,两个实数a,b的“a→b”运算原理如图所示,若f(x)=(0→x)•x-(2→x),则y=f(x)在x∈[-2,2]时的最小值是( )
定义一种运算符号“→”,两个实数a,b的“a→b”运算原理如图所示,若f(x)=(0→x)•x-(2→x),则y=f(x)在x∈[-2,2]时的最小值是( )| A. | -8 | B. | $-\frac{1}{4}$ | C. | -2 | D. | -6 |
3.设函数f(x)=$\frac{2}{x}$+lnx则( )
| A. | x=2为f(x)的极小值点 | B. | x=2为f(x)的极大值点 | ||
| C. | $x=\frac{1}{2}$为f(x)的极小值点 | D. | $x=\frac{1}{2}$为f(x)的极大值点 |
10.从5名男生医生、2名女医生中选3名医生组成一个医疗小分队,要求其中至少有1名女医生,则不同的组队方案共有( )
| A. | 30种 | B. | 25种 | C. | 20种 | D. | 10种 |
 ,在0处的导数为27,则
,在0处的导数为27,则 ( )
( )