题目内容
13. 定义一种运算符号“→”,两个实数a,b的“a→b”运算原理如图所示,若f(x)=(0→x)•x-(2→x),则y=f(x)在x∈[-2,2]时的最小值是( )
定义一种运算符号“→”,两个实数a,b的“a→b”运算原理如图所示,若f(x)=(0→x)•x-(2→x),则y=f(x)在x∈[-2,2]时的最小值是( )| A. | -8 | B. | $-\frac{1}{4}$ | C. | -2 | D. | -6 |
分析 通过程序框图判断出S=a→b的解析式,再求出f(x)的解析式,从而求出f(2)的值,最后根据所求出f(x)的解析式结合图象求解f(x)在区间[-2,2]上的最小值即可.
解答 解:∵由流程图可知,运算P=a→b中P的值等于分段函数 P=$\left\{\begin{array}{l}{|b|}&{a≥b}\\{a}&{a<b}\end{array}\right.$的函数值,
∴f(x)=(0→x)x-(2→x)=$\left\{\begin{array}{l}{\stackrel{-{x}^{2}+x}{-x}}&{\stackrel{x≤0}{0<x≤2}}\\{-2}&{x>2}\end{array}\right.$,
画出它的图象,如图所示,
由图可知,当x=-2时,f(x)在区间[-2,2]上的最小值为-6.
故选:D.
点评 本题考查判断程序框图的功能即判断出新运算法则,利用运算法则求值,解决新定义题关键是理解题中给的新定义,属于中档题.

练习册系列答案
相关题目
7.已知函数f(x)是定义在R上的偶函数,且在区间[0,+∞)上单调递减,若实数a满足$f({log_2}a)+f({log_{\frac{1}{2}}}a)≤2f(1)$,则实数a的取值范围是( )
| A. | (0,2] | B. | $[\frac{1}{2},2]$ | C. | [2,+∞) | D. | $(0,\frac{1}{2}]∪[{2,+∞})$ |
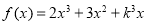 ,在0处的导数为27,则
,在0处的导数为27,则 ( )
( ) 已知一个锥体的主视图和左视图如图所示,下列选项中,不可能是该锥体的俯视图的是( )
已知一个锥体的主视图和左视图如图所示,下列选项中,不可能是该锥体的俯视图的是( )



 如图,在△ABC中,∠C=90°,∠ABC平分线BE交AC于点E,点D在AB上,∠DEB=90°.
如图,在△ABC中,∠C=90°,∠ABC平分线BE交AC于点E,点D在AB上,∠DEB=90°.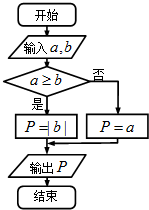 定义一种运算符号“→”,两个实数a,b的“a→b”运算原理如图所示,若函数f(x)=2→x,则f(2)+f(-2)=( )
定义一种运算符号“→”,两个实数a,b的“a→b”运算原理如图所示,若函数f(x)=2→x,则f(2)+f(-2)=( )