题目内容
11.已知f(x)=2cos$\frac{x}{2}$($\sqrt{3}$cos$\frac{x}{2}$-sin$\frac{x}{2}$).(1)求f(x)的单调递增区间;
(2)在△ABC中,AB=1,f(C)=$\sqrt{3}$+1,S△ABC=$\frac{\sqrt{3}}{2}$,求sinA+sinB.
分析 (1)由三角函数恒等变换化简函数解析式可得:f(x)=-2sin(x-$\frac{π}{3}$)+$\sqrt{3}$,由2kπ+$\frac{π}{2}$≤x-$\frac{π}{3}$≤2kπ$+\frac{3π}{2}$,k∈Z可解得f(x)的单调递增区间.
(2)由f(C)=$\sqrt{3}+1$,结合C的范围,可求C的大小,由S△ABC=$\frac{\sqrt{3}}{2}$可求ab,由余弦定理可求a2+b2=7,从而可得a+b=$\sqrt{3}+2$,由正弦定理即可得解.
解答 解:(1)f(x)=$\sqrt{3}$+$\sqrt{3}$cosx-sinx=-2sin(x-$\frac{π}{3}$)+$\sqrt{3}$,…(3分)
∴由2kπ+$\frac{π}{2}$≤x-$\frac{π}{3}$≤2kπ$+\frac{3π}{2}$,k∈Z可解得f(x)的单调递增区间为[2kπ+$\frac{5π}{6}$,2kπ$+\frac{11π}{6}$],k∈Z…(5分)
(2)由f(C)=-2sin(C-$\frac{π}{3}$)+$\sqrt{3}$=$\sqrt{3}+1$,可得sin(C-$\frac{π}{3}$)=-$\frac{1}{2}$,
∵0<C<π,可得-$\frac{π}{3}$<C-$\frac{π}{3}$<$\frac{2π}{3}$
∴可解得:C=$\frac{π}{6}$,
由S△ABC=$\frac{1}{2}$absinC=$\frac{\sqrt{3}}{2}$有ab=2$\sqrt{3}$,
由c2=a2+b2-2abcosC有a2+b2=7,…(8分)
∴a+b=$\sqrt{3}+2$,…(10分)
∴sinA+sinB=$\frac{(a+b)sinC}{c}$=1+$\frac{\sqrt{3}}{2}$…(12分)
点评 本题主要考查了三角函数恒等变换,三角函数的图象与性质,余弦定理,正弦定理以及三角形面积公式的应用,熟练掌握相关定理是解题的关键,属于基本知识的考查.

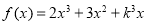 ,在0处的导数为27,则
,在0处的导数为27,则 ( )
( ) 如图,在△ABC中,∠C=90°,∠ABC平分线BE交AC于点E,点D在AB上,∠DEB=90°.
如图,在△ABC中,∠C=90°,∠ABC平分线BE交AC于点E,点D在AB上,∠DEB=90°.