题目内容
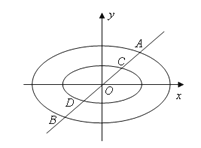
【题目】《周髀算经》中给出了弦图，所谓弦图是由四个全等的直角三角形和中间一个小正方形拼成一个大的正方形，若图中直角三角形两锐角分别为
，
，且小正方形与大正方形面积之比为
，则
的值为（ ）
A. 
B. 
C. 
D. 
【答案】D
【解析】
设大的正方形的边长为1，由已知可求小正方形的边长，可求cosα﹣sinα=
，sinβ﹣cosβ=，且cosα=sinβ，sinα=cosβ，进而利用两角差的余弦函数公式，同角三角函数基本关系式即可计算得解．
设大的正方形的边长为1，由于小正方形与大正方形面积之比为9：25，
可得：小正方形的边长为，
可得：cosα﹣sinα=，①sinβ﹣cosβ=，②
由图可得：cosα=sinβ，sinα=cosβ，
①×②可得：
=cosαsinβ+sinαcosβ﹣cosαcosβ﹣sinαsinβ=sin2β+cos2β﹣cos（α﹣β）=1﹣cos（α﹣β），
解得：cos（α﹣β）=
．
故选：D．
练习册系列答案
阅读快车系列答案
相关题目
【题目】已知函数
的定义域为
，部分对应值如下表．
x |
| 0 | 4 | 5 |
| 1 | 2 | 2 | 1 |
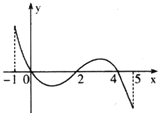
的导函数
的图象如图所示：下列关于的命题：
函数是周期函数；
函数在
是减函数；
如果当
时，的最大值是2，那么t的最大值为4；
函数
的零点个数可能为0、1、2、3、4个．
其中正确命题的序号是______．
