��Ŀ����
����Ŀ�����壺����Բ����������Ͷ����һ��������ɵ������γ�Ϊ����Բ���������������������������Բ���������������������Ƶģ������������Բ����������Բ�������������ε����Ʊȳ�Ϊ��Բ�����Ʊȣ���֪��Բ![]() ��
��
��1������Բ![]() ���ж�
���ж�![]() ��
��![]() �Ƿ����ƣ�������ƣ����
�Ƿ����ƣ�������ƣ����![]() ��
��![]() �����Ʊȣ���������ƣ���˵�����ɣ�
�����Ʊȣ���������ƣ���˵�����ɣ�
��2��д������Բ![]() �����ҽ�����
�����ҽ�����![]() ���ϡ��̰��᳤Ϊ
���ϡ��̰��᳤Ϊ![]() ����Բ
����Բ![]() �ı����̣�������Բ
�ı����̣�������Բ![]() �ϴ�������
�ϴ�������![]() ��
��![]() ����ֱ��
����ֱ��![]() �Գƣ���ʵ��
�Գƣ���ʵ��![]() ��ȡֵ��Χ��
��ȡֵ��Χ��
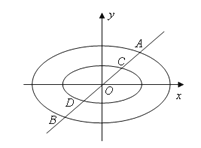
��3����ͼ��ֱ��![]() ��������������Բ��
��������������Բ��![]() ��
��![]() �ֱ��ڵ�
�ֱ��ڵ�![]() �͵�
�͵�![]() ��������Բ
��������Բ![]() ����Բ
����Բ![]() �Ϸֱ�������
�Ϸֱ�������![]() �͵�
�͵�![]() ������Բ���㣩��ʹ
������Բ���㣩��ʹ![]() ��
��![]() �����
�����![]() Ϊ���Ʊȵ��������������Σ�д������������������֤����
Ϊ���Ʊȵ��������������Σ�д������������������֤����
���𰸡���1�� ���Ʊ�Ϊ![]() ��2��
��2��![]() ��3���������
��3���������
��������
��1����Բ![]() ��
��![]() ���ƣ�
���ƣ�
��Ϊ��Բ![]() ������������������Ϊ4���ױ߳�Ϊ
������������������Ϊ4���ױ߳�Ϊ![]() �ĵ��������Σ�
�ĵ��������Σ�
����Բ![]() ������������������Ϊ2���ױ߳�Ϊ
������������������Ϊ2���ױ߳�Ϊ![]() �ĵ��������Σ�
�ĵ��������Σ�
��������������������ƣ������Ʊ�Ϊ![]()
��2����Բ![]() �ķ���Ϊ��
�ķ���Ϊ��![]()
��![]() ����
����![]() ��
��![]() �е�Ϊ
�е�Ϊ![]() ��
��
��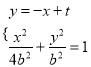 ������
������![]()
��![]()
��Ϊ�е���ֱ��![]() �ϣ�������
�ϣ�������![]() ��
��![]()
��ֱ��![]() �ķ���Ϊ��
�ķ���Ϊ��![]() ��
��
�������֪��ֱ��![]() ����Բ
����Բ![]() ��������ͬ�Ľ��㣬
��������ͬ�Ľ��㣬
������![]() ��������ͬ��ʵ���⣬
��������ͬ��ʵ���⣬
����![]() ����
����![]()
��3������1����ԭ����ֱ��![]() ������Բ
������Բ![]() ����Բ
����Բ![]() �ڵ�
�ڵ�![]() �͵�
�͵�![]() ����
����![]() ��
��![]() ��Ϊ�������������Σ������Ʊ�Ϊ
��Ϊ�������������Σ������Ʊ�Ϊ![]() ��
��
����2������A����C�ֱ���![]() �ᣨ��
�ᣨ��![]() �ᣩ�Ĵ��ߣ�����Բ
�ᣩ�Ĵ��ߣ�����Բ![]() ����Բ
����Բ![]() �ڵ�
�ڵ�![]() �͵�
�͵�![]() ����
����![]() ��
��![]() ��Ϊ�������������Σ������Ʊ�Ϊ
��Ϊ�������������Σ������Ʊ�Ϊ![]() ��
��

 ��������һ���þ�ϵ�д�
��������һ���þ�ϵ�д� Сѧ��10����Ӧ����ϵ�д�
Сѧ��10����Ӧ����ϵ�д�