题目内容

在△ABC中，点D是BC中点，若∠A=60°，
AB
•
AC
=
1
2
，则|
AD
|的最小值是（　　）
A、
3
2
B、
2
2
C、
3
4
D、
3
2
考点：平面向量数量积的运算
专题：平面向量及应用
分析：利用向量的平行四边形法则、数量积运算、基本不等式即可得出．
解答： 解：如图所示，
∵∠A=60°，
AB
•
AC
=
1
2
，
∴|
AB
|•|
AC
|cos60°=
1
2
，
∴cb=1．
在△ABC中，点D是BC中点，
∴2
AD
=
AB
+
AC
，
∴4
AD
2=
AB
2+
AC
2+2
AB
•
AC
=
=c2+b2+1≥2bc+1=3，当且仅当b=c=1时取等号．
∴∴|
AD
|≥
3
2

∴|
AD
|的最小值是
3
2
，
故选：A
点评：本题考查了向量的平行四边形法则、数量积运算、基本不等式，属于中档题．
练习册系列答案
相关题目
已知集合M={x|x≤0}，N={-2，0，1}，则M∩N=（　　）
A、{x|x≤0}
B、{-2，0}
C、{x|-2≤x≤0}
D、{0，1}
已知函数f（x）=ex-ax-a（其中a∈R，e是自然对数的底数，e=2.71828…）．
（Ⅰ）当a=e时，求函数f（x）的极值；
（Ⅱ）若f（x）≥0恒成立，求实数a的取值范围．
已知△ABC中，若
BC
2=|
AC
|•|
AB
|，2
AB
•
AC
=
BA
•
BC
+
CA
•
CB
，求角A．
已知
i
与
j
为互相垂直的单位向量，
a
=
i
-2
j
，
b
=
i
+λ
j
且
a
与
b
的夹角为锐角，则实数λ的取值范围是（　　）
A、（-∞，
1
2
）
B、（
1
2
，+∞）
C、（-2，
2
3
）∪（
2
3
，+∞）
D、（-∞，-2）∪（-2，
1
2
）
已知f（logax）=
a
a2-1
（x-
1
x
）（a＞0，且a≠1）
（1）求f（x）的解析式；
（2）判断并证明f（x）的奇偶性与单调性；
（3）若不等式f（3t2-1）+f（4t-k）＞0对任意t∈[1，3]都成立，求实数k的取值范围．
按照程序框图执行，第3个输出的数是（　　）
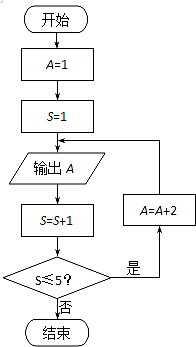
A、4B、5C、6D、7
求极限
lim
x→0
(1-cosx)[x-ln(1+tanx)]
sin4x
．
已知复数z1=1+i，z2=
1
1+i
在复平面内对应的点分别为P1、P2，O为坐标原点，则向量
OP1
、
OP2
所成的角为（　　）
A、
π
6
B、
π
4
C、
π
3
D、
π
2

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网