题目内容
双曲线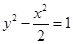 的渐近线方程为( )
的渐近线方程为( )
A.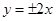 | B.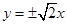 | C.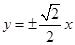 | D.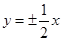 |
C
解析试题分析:由于双曲线的方程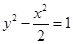 ,那么可知焦点在y轴上,那么渐进线方程为y=
,那么可知焦点在y轴上,那么渐进线方程为y= ,而方程中a2=1,b2=2,那么可知a=1,b=
,而方程中a2=1,b2=2,那么可知a=1,b= ,得到结论为
,得到结论为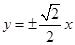 ,选C
,选C
考点:本试题主要考查了双曲线的结合性质中渐近线的求解,是一道基础题。
点评:解决该试题的关键是能根据已知方程表示出a,b的值,同时能确定焦点的位置,进而得到渐近线方程。

练习册系列答案
相关题目
已知抛物线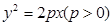 的焦点弦
的焦点弦 坐标分别为
坐标分别为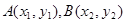 ,则
,则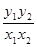 的值一定等于( )
的值一定等于( )
A.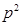 | B. | C. | D. |
若 和F分别为椭圆
和F分别为椭圆
 的中心和左焦点,点P为椭圆上的任意点,则
的中心和左焦点,点P为椭圆上的任意点,则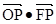 的最大值是( )
的最大值是( )
| A. 2 | B.3 | C. 6 | D. 8 |
已知双曲线方程为 ,过
,过 的直线
的直线 与双曲线只有一个公共点,则
与双曲线只有一个公共点,则 的条数共有( )
的条数共有( )
| A.4条 | B.3条 | C.2条 | D.1条 |
已知直线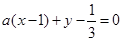
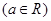 和椭圆
和椭圆 ,则直线和椭圆相交有( )
,则直线和椭圆相交有( )
| A.两个交点 | B.一个交点 | C.没有交点 | D.无法判断 |
已知抛物线 ,过点
,过点 )作倾斜角为
)作倾斜角为 的直线
的直线 ,若
,若 与抛物线交于
与抛物线交于 、
、 两点,弦
两点,弦 的中点
的中点 到y轴的距离为( )
到y轴的距离为( )
A. | B. | C. | D. |
已知双曲线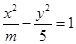 (
(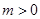 )的右焦点与抛物线
)的右焦点与抛物线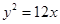 的焦点相同,则此双曲线的离心率为( )
的焦点相同,则此双曲线的离心率为( )
A.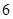 | B.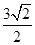 | C.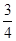 | D.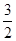 |
抛物线 的准线方程是( )
的准线方程是( )
A. | B. | C. | D. |
 ,对于任意实数
,对于任意实数 下列直线被椭圆E截得的弦长与直线
下列直线被椭圆E截得的弦长与直线 被椭圆E截得的弦长不可能相等的是( )
被椭圆E截得的弦长不可能相等的是( )


