题目内容
6.已知圆M:x2+(y-1)2=1,圆N:x2+(y+1)2=1,直线l1、l2分别过圆心M、N,且l1与圆M相交于A、B,l2与圆N相交于C、D,P是椭圆$\frac{x^2}{3}+\frac{y^2}{4}$=1上的任意一动点,则$\overrightarrow{PA}•\overrightarrow{PB}+\overrightarrow{PC}•\overrightarrow{PD}$的最小值为( )| A. | $\sqrt{3}$ | B. | 2$\sqrt{3}$ | C. | 3 | D. | 6 |
分析 如图所示,圆心M(0,1),N(0,-1)即为椭圆的焦点.$\overrightarrow{PA}=\overrightarrow{PM}+\overrightarrow{MA}$,$\overrightarrow{PB}=\overrightarrow{PM}+\overrightarrow{MB}$,$\overrightarrow{MA}+\overrightarrow{MB}=\overrightarrow{0}$,可得$\overrightarrow{PA}•\overrightarrow{PB}$=${\overrightarrow{PM}}^{2}$-1,$\overrightarrow{PC}•\overrightarrow{PD}$=${\overrightarrow{PN}}^{2}$-1,由于|PM|+|PN|=4,利用2(${\overrightarrow{PM}}^{2}$+${\overrightarrow{PN}}^{2}$)≥$(|\overrightarrow{PM}|+|\overrightarrow{PN}|)^{2}$,即可得出.
解答 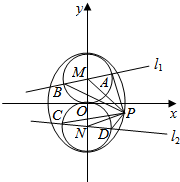 解:如图所示,
解:如图所示,
圆心M(0,1),N(0,-1)即为椭圆的焦点.
$\overrightarrow{PA}=\overrightarrow{PM}+\overrightarrow{MA}$,$\overrightarrow{PB}=\overrightarrow{PM}+\overrightarrow{MB}$,$\overrightarrow{MA}+\overrightarrow{MB}=\overrightarrow{0}$,
∴$\overrightarrow{PA}•\overrightarrow{PB}$=${\overrightarrow{PM}}^{2}$+$\overrightarrow{MA}•\overrightarrow{MB}$=${\overrightarrow{PM}}^{2}$-1,
$\overrightarrow{PC}•\overrightarrow{PD}$=${\overrightarrow{PN}}^{2}$-1,
∴$\overrightarrow{PA}•\overrightarrow{PB}+\overrightarrow{PC}•\overrightarrow{PD}$=${\overrightarrow{PM}}^{2}$+${\overrightarrow{PN}}^{2}$-2,
∵|PM|+|PN|=4,
∴2(${\overrightarrow{PM}}^{2}$+${\overrightarrow{PN}}^{2}$)≥$(|\overrightarrow{PM}|+|\overrightarrow{PN}|)^{2}$=16,当且仅当|PM|=|PN|=2时取等号.
∴${\overrightarrow{PM}}^{2}$+${\overrightarrow{PN}}^{2}$≥8,
∴$\overrightarrow{PA}•\overrightarrow{PB}+\overrightarrow{PC}•\overrightarrow{PD}$=${\overrightarrow{PM}}^{2}$+${\overrightarrow{PN}}^{2}$-2≥6,
故选:D.
点评 本题考查了椭圆的标准方程及其性质、圆的标准方程及其性质、向量的三角形法则、基本不等式的性质、数量积运算性质,考查了推理能力与计算能力,属于难题.

| A. | -3+4i | B. | 0 | C. | -4+3i | D. | -4-3i |
| A. | 2 | B. | $2\sqrt{2}$ | C. | 4 | D. | $4\sqrt{2}$ |
| A. | 充分不必要 | B. | 必要不充分 | ||
| C. | 充要条件 | D. | 既不充分也不必要 |
| A. | 6-4$\sqrt{2}$ | B. | 3-2$\sqrt{2}$ | C. | 2$\sqrt{2}$-3 | D. | 4$\sqrt{2}$-6 |
| A. | 充分而不必要条件 | B. | 必要而不充分条件 | ||
| C. | 充分必要条件 | D. | 既不充分也不必要条件 |
