题目内容
已知平面区域Ω={(x,y)|
|
|
分析:先利用线性规划的知识作出平面区域Ω,M,根据图象分别计算面积,然后代入几何概率的计算公式可求
解答:解:构成试验的全部区域为Ω为图中的三角形ABC,A(-1,0)B(1,0)C(1,2),面积为S△ABC =
×2×2=2
基本事件点P落在区域M为图中的△ABM,面积为
×2×1=1
代入几何概率的计算公式可得P=
故答案为:

| 1 |
| 2 |
基本事件点P落在区域M为图中的△ABM,面积为
| 1 |
| 2 |
代入几何概率的计算公式可得P=
| 1 |
| 2 |
故答案为:
| 1 |
| 2 |

点评:本题考查了与面积有关的几何概率的求解,还考查了不等式表示平面区域及平面区域的面积求解,属于综合试题.

练习册系列答案
 中考利剑中考试卷汇编系列答案
中考利剑中考试卷汇编系列答案 教育世家状元卷系列答案
教育世家状元卷系列答案 黄冈课堂作业本系列答案
黄冈课堂作业本系列答案 单元加期末复习先锋大考卷系列答案
单元加期末复习先锋大考卷系列答案
相关题目
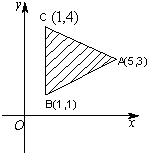 已知平面区域如图所示,z=x+my(m>0)在平面区域内取得最大值时的解(x,y)有无数多个,则m=
已知平面区域如图所示,z=x+my(m>0)在平面区域内取得最大值时的解(x,y)有无数多个,则m=