题目内容
在平面直角坐标系xOy,已知平面区域 A={ (x,y)|x+ty<2,且t∈R,x≥0,y≥0},若平面区域B={ (x,y )|(x+y,x-y )∈A }的面积不小于1,则t的取值范围为分析:由题意可知平面区域B={ (x,y )|(x+y,x-y )∈A }中的x+y相当于平面区域 A中的x.平面区域B中的y相当于平面区域 A中的y,所以可得
,再求出这个不等式组表示的平面区域的面积,此面积大于等于1,解出t即可.
|
解答:解:∵B={ (x,y )|(x+y,x-y )∈A },∴
由
得交点坐标(
,-
)
由
,的交点坐标(1,1)
又∵x+y=0与x-y=0交于(0,0)点,
∴平面区域B={ (x,y )|(x+y,x-y )∈A }的面积为
≥1
解得t2≤1,-1≤t≤1
故答案为-1≤t≤1
|
由
|
| 1 |
| t |
| 1 |
| t |
由
|
又∵x+y=0与x-y=0交于(0,0)点,
∴平面区域B={ (x,y )|(x+y,x-y )∈A }的面积为
| 1 |
| 2 |
(
|
| 2 |
解得t2≤1,-1≤t≤1
故答案为-1≤t≤1
点评:本题考查了二元一次不等式组表示的平面区域的面积的求法,做题时要认真分析,找到两个平面区域的联系.

练习册系列答案
相关题目
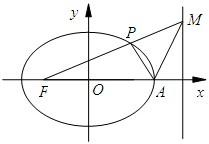 如图,在平面直角坐标系xOy中,椭圆C:
如图,在平面直角坐标系xOy中,椭圆C: