题目内容
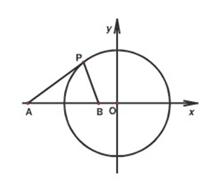
已知圆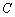 :
: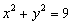 ,点
,点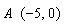 ,直线
,直线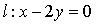 .
.
(1)求与圆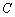 相切,且与直线
相切,且与直线 垂直的直线方程;
垂直的直线方程;
(2)在直线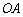 上(
上(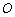 为坐标原点),存在定点
为坐标原点),存在定点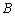 (不同于点
(不同于点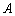 ),满足:对于圆
),满足:对于圆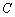 上的任一点
上的任一点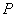 ,都有
,都有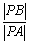 为一常数,试求出所有满足条件的点
为一常数,试求出所有满足条件的点 的坐标.
的坐标.
(1)设所求直线方程为 ,即
,即 .
.
由直线与圆相切,可知 ,得
,得 ,
,
故所求直线方程为
(2)方法1:假设存在这样的点 ,
,
当 为圆
为圆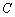 与
与 轴左交点
轴左交点 时,
时, ,
,
当 为圆
为圆 与
与 轴右交点
轴右交点 时,
时,
依题意, ,解得
,解得 (舍去),或
(舍去),或 .
.
下面证明:点 对于圆
对于圆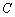 上任一点
上任一点 ,都有
,都有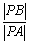 为一常数.
为一常数.
设 ,则
,则 .
.
 ,
,
从而 为常数.
为常数.
方法2:假设存在这样的点 ,使得
,使得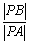 为常数
为常数 ,则
,则 ,
,
于是 ,将
,将 代入得,
代入得,
 ,即
,即
 对
对 恒成立,
恒成立,
所以 ,解得
,解得 或
或 (舍去),
(舍去),
故存在点 对于圆
对于圆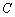 上任一点
上任一点 ,都有
,都有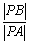 为一常数
为一常数 .
.
|

练习册系列答案
相关题目

 满足:
满足: ,且对于任意的
,且对于任意的 ,都有
,都有 ,则不等式
,则不等式 的解集为 __________________
的解集为 __________________ ,则
,则 = .
= . ,且与以
,且与以 ,
, 为端点的线段(包含端点)有交点,则直线
为端点的线段(包含端点)有交点,则直线 的取值范围是( )
的取值范围是( ) B.
B. C.
C. D.
D.
 的最大值为 ( )
的最大值为 ( ) 
 的单调递减区间是____
的单调递减区间是____