题目内容
已知双曲线
-
=1(a>0)的右焦点与抛物线y2=12x的焦点重合,则过该双曲线的左顶点且与直线y=2x+1平行的直线方程是( )
| x2 |
| a2 |
| y2 |
| 4 |
A、y=-
| ||||
B、y=-
| ||||
C、y=2x+2
| ||||
| D、y=2x+10 |
考点:双曲线的简单性质
专题:圆锥曲线的定义、性质与方程
分析:根据双曲线和抛物线的性质,求出a的值,再根据该直线与直线y=2x+1平行,且过点(-
,0),求得该直线方程.
| 5 |
解答:
解:由题意得抛物线y2=12x的焦点坐标为(3,0)
∵双曲线
-
=1(a>0)的右焦点与抛物线y2=12x的焦点重合,
∴a2+4=32
解得,a=
,
∴该双曲线的左顶点坐标为(-
,0),
又过该双曲线的左顶点且与直线y=2x+1平行,
∴y=2(x+
)
即y=2x+2
.
故选:C.
∵双曲线
| x2 |
| a2 |
| y2 |
| 4 |
∴a2+4=32
解得,a=
| 5 |
∴该双曲线的左顶点坐标为(-
| 5 |
又过该双曲线的左顶点且与直线y=2x+1平行,
∴y=2(x+
| 5 |
即y=2x+2
| 5 |
故选:C.
点评:本题主要考查了双曲线和抛物线的性质,以及线线平行的性质,属于中档题.

练习册系列答案
相关题目
为了了解儿子与其父亲身高的关系,随机抽取5对父子的身高数据如下:
则y关于x的线性回归方程必通过以下哪个点( )
| 父亲身高x | 174 | 176 | 176 | 176 | 178 |
| 儿子身高y | 175 | 175 | 176 | 177 | 177 |
| A、(174,175) |
| B、(176,175) |
| C、(174,176) |
| D、(176,176) |
椭圆C:
+
=1(a>b>0)和双曲线D:
-
=1(A>0,B>0)有相同的焦点F1、F2,椭圆C和双曲线D在第一象限内的交点为P,且PF2垂直于x轴.设椭圆的离心率为e1,双曲线D的离心率为e2,则e1e2等于( )
| x2 |
| a2 |
| y2 |
| b2 |
| x2 |
| A2 |
| y2 |
| B2 |
| A、1 | ||
B、
| ||
C、
| ||
| D、不确定 |
要得到函数y=cosx的图象,只需将函数y=cos(x+
)的图象沿x轴( )
| π |
| 4 |
A、向左平移
| ||
B、向左平移
| ||
C、向右平移
| ||
D、向右平移
|
下列说法不正确的是( )
| A、一个命题与它的逆命题、否命题、逆否命题等四种命题中真命题个数为偶数 | ||||||||
| B、命题:“若xy=0,则x=0或y=0”的逆否命题是“若x≠0且y≠0,则xy≠0” | ||||||||
C、椭圆
| ||||||||
D、已知直线l1:ax+3y-1=0,l2:x+by+1=0,则l1⊥l2的充分不必要条件是
|
方程y=k(x-2)表示( )
| A、过点(-2,0)的一切直线 |
| B、过点(2,0)的一切直线 |
| C、过点(2,0)且不垂直于x轴的一切直线 |
| D、过点(2,0)且除去x轴的一切直线 |
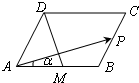 在平行四边形ABCD中,AB=2,AD=1,∠DAB=60°,点M为AB的中点,点P从B→C→D(含端点),设∠PAB=α,记tanα=x,
在平行四边形ABCD中,AB=2,AD=1,∠DAB=60°,点M为AB的中点,点P从B→C→D(含端点),设∠PAB=α,记tanα=x,| AP |
| DM |
A、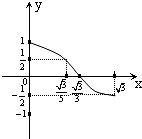 |
B、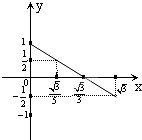 |
C、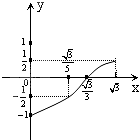 |
D、 |
在△ABC中,A=60°,b=1,且面积为
,则
=( )
| 3 |
| 2a+2b-2c |
| sinA+sinB-sinC |
A、
| ||||
B、
| ||||
C、
| ||||
D、4
|