题目内容
若
=________．
1
分析：把已知条件移项得到tanα与tanβ的和与积的关系式，根据α+β的范围得到tan（α+β）的值存在，所以利用两角和的正切函数公式化简后，利用tanα与tanβ的和与积的关系式可得值．
解答：由tanαtanβ+tanα+tanβ=1移项得：tanα+tanβ=1-tanαtanβ，
因为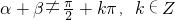
，则tan（α+β）=
=1
故答案为1．
点评：考查学生灵活运用两角和与差的正切函数公式，注意角度的范围．
分析：把已知条件移项得到tanα与tanβ的和与积的关系式，根据α+β的范围得到tan（α+β）的值存在，所以利用两角和的正切函数公式化简后，利用tanα与tanβ的和与积的关系式可得值．
解答：由tanαtanβ+tanα+tanβ=1移项得：tanα+tanβ=1-tanαtanβ，
因为
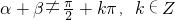，则tan（α+β）==1故答案为1．
点评：考查学生灵活运用两角和与差的正切函数公式，注意角度的范围．
练习册系列答案
相关题目
若双曲线
-
=1（a＞b＞0）的左右焦点分别为F1、F2，线段F1F2被抛物线y2=2bx的焦点分成7：5的两段，则此双曲线的离心率为（ ）
| x2 |
| a2 |
| y2 |
| b2 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|