题目内容
已知抛物线 的焦点F和椭圆
的焦点F和椭圆 的右焦点重合.
的右焦点重合.
(1)求抛物线 的方程;
的方程;
(2)若定长为5的线段 两个端点在抛物线
两个端点在抛物线 上移动,线段
上移动,线段 的中点为
的中点为 ,求点
,求点 到y轴的最短距离,并求此时
到y轴的最短距离,并求此时 点坐标.
点坐标.
解:(1)∵椭圆的右焦点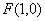 ,
,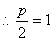 ,即
,即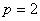 .
.
∴抛物线 的方程为
的方程为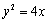
(2)要求 点到y轴距离最小值,只要求出
点到y轴距离最小值,只要求出 点到抛物线准线的距离最小值即可.过
点到抛物线准线的距离最小值即可.过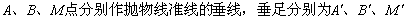 ,设焦点为F.
,设焦点为F.
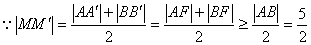 ,当且仅当线段
,当且仅当线段 过焦点F时取等号.∴
过焦点F时取等号.∴ 点到y轴的最短距离为
点到y轴的最短距离为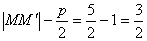 ;
;
设此时中点 的坐标为(
的坐标为(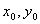 ),则
),则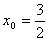 ,设
,设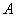
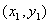 ,
,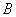
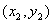 ,则
,则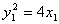 ,
,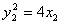 ,两式相减得:
,两式相减得: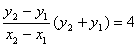 ,即
,即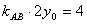 ,
,
∴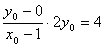 ,∴
,∴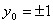 ,∴此时
,∴此时 点坐标为
点坐标为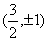

练习册系列答案
 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案
相关题目
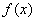 满足
满足 ,且
,且 ,则不等式
,则不等式 .
. 的三角形区域内随机投一点M,则该点M与三角形三个顶点距离都大于1的概率为 ( )
的三角形区域内随机投一点M,则该点M与三角形三个顶点距离都大于1的概率为 ( )  B.
B.  C.
C.  D.
D. 
 在
在 上存在导数
上存在导数 ,
, ,有
,有 ,
, 上
上 ,若
,若 ,则实数
,则实数 的取值范围是_____________.
的取值范围是_____________.  ,则事件“
,则事件“ ”发生的概率为
”发生的概率为 B.
B. C.
C. D.
D.
 ,若△ABC面积的最大值为
,若△ABC面积的最大值为 ,则
,则 的值为
的值为 上的函数
上的函数 满足
满足 ,当
,当 时,
时, ,当
,当 时,
时, .则
.则 =( )
=( ) =3,则
=3,则 =
= 
 ( )
( ) C.
C. D.3
D.3