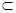题目内容
三棱锥P?ABC中,PA⊥平面ABC,AB⊥BC。
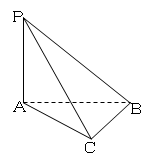
(1)证明:平面PAB⊥平面PBC;
(2)若PA=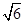 ,PC与侧面APB所成角的余弦值为
,PC与侧面APB所成角的余弦值为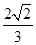 ,PB与底面ABC成60°角,求二面角B―PC―A的大小。
,PB与底面ABC成60°角,求二面角B―PC―A的大小。

(1)证明:平面PAB⊥平面PBC;
(2)若PA=
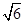 ,PC与侧面APB所成角的余弦值为
,PC与侧面APB所成角的余弦值为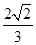 ,PB与底面ABC成60°角,求二面角B―PC―A的大小。
,PB与底面ABC成60°角,求二面角B―PC―A的大小。(1)证明详见解析;(2)60°
试题分析:(Ⅰ)先利用线面垂直的判定定理证明BC⊥平面PAB,再利用面面垂直的判定定理证明平面PAB⊥平面PBC;(2)过A作
 则ÐEFA为所求.然后求出AB=
则ÐEFA为所求.然后求出AB= ,PB=2
,PB=2 ,PC=3及AE,AF,在Rt
,PC=3及AE,AF,在Rt AEF中求解即可.
AEF中求解即可.试题解析: (1)证明:∵PA^面ABC,\PA^BC, ∵AB^BC,且PA∩AB=A,\BC^面PAB
而BCÌ面PBC中,\面PAB^面PBC. ……5分
(2)过A作


则ÐEFA为B?PC?A的二面角的平面角 8分
由PA=
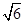 ,在RtDPBC中,cosÐCPB=
,在RtDPBC中,cosÐCPB=
 .
.RtDPAB中,ÐPBA=60°. \AB=
 ,PB=2
,PB=2 ,PC=3 \AE=
,PC=3 \AE=  =
= 
同理:AF=
 10分
10分∴sin
 =
= =
= , 11分
, 11分∴
 =60°. 12分
=60°. 12分另解:向量法:由题可知:AB=
 ,BC=1,建立如图所示的空间直角坐标系 7分
,BC=1,建立如图所示的空间直角坐标系 7分B(0,0,0),C(1,0,0),A(0,
 ,0),P(0,
,0),P(0, ,
,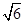 ),假设平面BPC的法向量为
),假设平面BPC的法向量为 =(x1,y1,z1),
=(x1,y1,z1),∴

取z1=
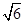 ,可得平面BPC法向量为
,可得平面BPC法向量为 =(0,?3
=(0,?3 ,
,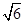 ) 9分
) 9分同理PCA的法向量为
 =(2,?
=(2,? ,0) 11分
,0) 11分∴cos<
 ,
, >=
>= =
= ,
, 所求的角为60° 12分
所求的角为60° 12分

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
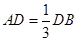 ,点C为圆O上一点,且
,点C为圆O上一点,且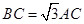 .点P在圆O所在平面上的正投影为点D,PD=DB.
.点P在圆O所在平面上的正投影为点D,PD=DB.
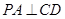 ;
;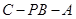 的余弦值.
的余弦值.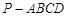 中,底面
中,底面 是平行四边形,
是平行四边形,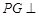 平面
平面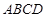 ,垂足为
,垂足为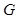 ,
,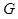 在
在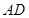 上且
上且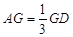 ,
,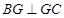 ,
,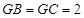 ,
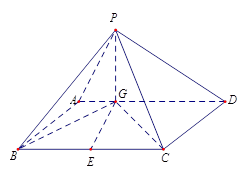
, 是
是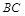 的中点,四面体
的中点,四面体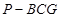 的体积为
的体积为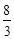 .
.
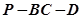 的正切值;
的正切值;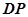 到平面
到平面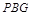 所成角的正弦值;
所成角的正弦值;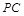 上是否存在一点
上是否存在一点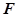 ,使异面直线
,使异面直线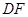 与
与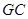 所成的角为
所成的角为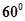 ,若存在,确定点
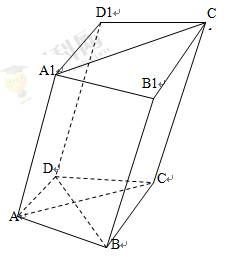
,若存在,确定点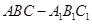 是一个斜三棱柱,已知
是一个斜三棱柱,已知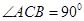 、平面
、平面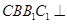 平面
平面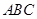 、
、 、
、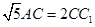 ,又
,又 、
、 分别是
分别是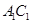 、
、 的中点.
的中点.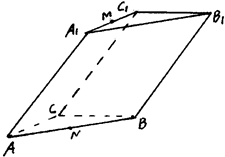
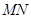 ∥平面
∥平面 ; (2)求二面角
; (2)求二面角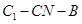 的大小.
的大小.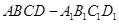 中,已知平面
中,已知平面 ,且
,且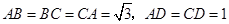 .
.
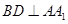 ;
;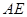 ∥平面
∥平面 ,求
,求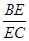 的值.
的值. 平面BCD(如图2),则下列结论中不正确的是( )
平面BCD(如图2),则下列结论中不正确的是( )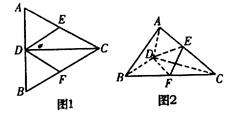
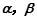 和两条不同直线
和两条不同直线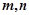 ,则下列说法正确的是( )
,则下列说法正确的是( )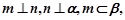 则
则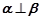
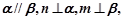 则
则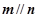
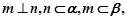 则
则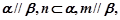 则
则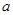 、
、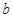 是两条不同直线,
是两条不同直线,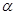 、
、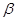 是两个不同平面,则下列命题错误的是( )
是两个不同平面,则下列命题错误的是( )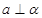 ,
,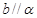 ,则
,则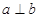
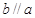 ,
,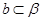 ,则
,则
 ,
,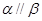 ,则
,则
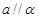 ,
,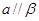 ,则
,则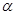 、
、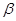 、
、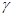 是不同的平面,给出下列命题:
是不同的平面,给出下列命题: