题目内容
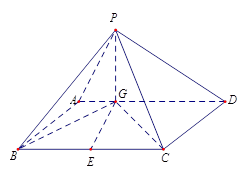
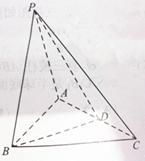
如图四棱锥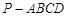 中,底面
中,底面 是平行四边形,
是平行四边形,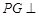 平面
平面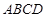 ,垂足为
,垂足为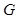 ,
,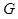 在
在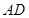 上且
上且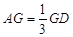 ,
,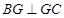 ,
,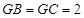 ,
,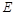 是
是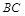 的中点,四面体
的中点,四面体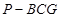 的体积为
的体积为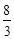 .
.
(1)求二面角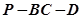 的正切值;
的正切值;
(2)求直线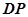 到平面
到平面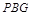 所成角的正弦值;
所成角的正弦值;
(3)在棱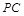 上是否存在一点
上是否存在一点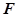 ,使异面直线
,使异面直线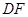 与
与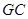 所成的角为
所成的角为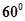 ,若存在,确定点
,若存在,确定点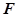 的位置,若不存在,说明理由.
的位置,若不存在,说明理由.
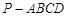 中,底面
中,底面 是平行四边形,
是平行四边形,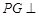 平面
平面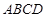 ,垂足为
,垂足为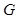 ,
,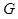 在
在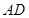 上且
上且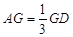 ,
,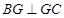 ,
,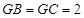 ,
,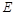 是
是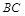 的中点,四面体
的中点,四面体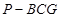 的体积为
的体积为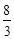 .
.
(1)求二面角
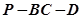 的正切值;
的正切值;(2)求直线
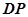 到平面
到平面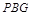 所成角的正弦值;
所成角的正弦值;(3)在棱
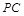 上是否存在一点
上是否存在一点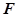 ,使异面直线
,使异面直线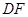 与
与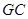 所成的角为
所成的角为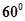 ,若存在,确定点
,若存在,确定点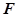 的位置,若不存在,说明理由.
的位置,若不存在,说明理由.(1)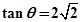 ;(2)
;(2)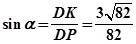 ;(3)不存在.
;(3)不存在.
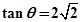 ;(2)
;(2)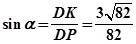 ;(3)不存在.
;(3)不存在.试题分析:(1)根据四面体
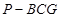 的体积及底面积可求出
的体积及底面积可求出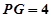 .
.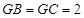 ,
, 为中点,所以
为中点,所以 ,这样可得
,这样可得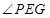 为二面角的平面角.在
为二面角的平面角.在 中即可求得其正切值.
中即可求得其正切值.(2)由于面
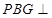 面
面 ,所以只需在面ABCD内过点D作交线BG的垂线,即可得PD在面PBG内的射影,从而得PD与面PBG所成的角.(3)存在性的问题,一般都通过建系来求.dsgjghmk
,所以只需在面ABCD内过点D作交线BG的垂线,即可得PD在面PBG内的射影,从而得PD与面PBG所成的角.(3)存在性的问题,一般都通过建系来求.dsgjghmk
 两两垂直,故可分别以
两两垂直,故可分别以 为
为 轴建立坐标系.
轴建立坐标系.假设
 存在且设
存在且设
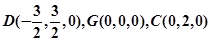
然后用向量的夹角公式求y,如果能求出满足条件的y则存在,若不能求出满足条件的y,则不存在.
试题解析:(1)由四面体
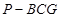 的体积为
的体积为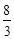 .∴
.∴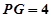
设二面角
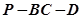 的大小为
的大小为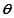
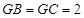
 为中点,
为中点,∴
 同理
同理 ∴
∴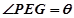
∴
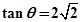 3分
3分(2)由
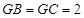
∴
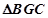 为等腰三角形,GE为
为等腰三角形,GE为 的角平分线,作
的角平分线,作 交BG的延长线于K,
交BG的延长线于K,∴

由平面几何知识可知:
 ,
,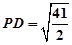 .设直线
.设直线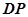 与平面
与平面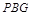 所成角为
所成角为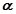
∴
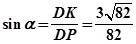 8分
8分(法二:建系)
(3)
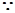
 两两垂直,分别以
两两垂直,分别以 为
为 轴建立坐标系
轴建立坐标系假设
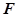 存在且设
存在且设
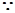
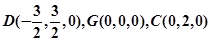
∴
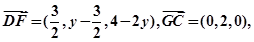 又直线
又直线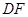 与
与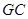 所成的角为
所成的角为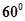
∴
 化简得:
化简得:
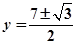 不满足
不满足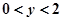
∴这样的点不存在 12分

练习册系列答案
 赢在课堂名师课时计划系列答案
赢在课堂名师课时计划系列答案 天天向上课时同步训练系列答案
天天向上课时同步训练系列答案 阳光课堂同步练习系列答案
阳光课堂同步练习系列答案
相关题目
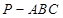 中,
中,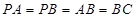 ,
,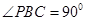 ,D为AC的中点,
,D为AC的中点,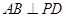 .
.
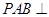 平面
平面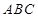 ;
;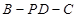 的余弦值.
的余弦值.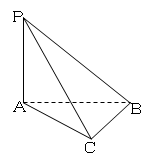
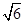 ,PC与侧面APB所成角的余弦值为
,PC与侧面APB所成角的余弦值为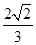 ,PB与底面ABC成60°角,求二面角B―PC―A的大小。
,PB与底面ABC成60°角,求二面角B―PC―A的大小。 的底面是正六边形,
的底面是正六边形,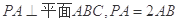 则下列结论正确的是( )
则下列结论正确的是( )


 ∥
∥
 所成的角为45°
所成的角为45°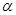 和
和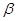 是两个不重合的平面,给出下列命题:
是两个不重合的平面,给出下列命题: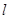 与
与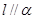 ;
;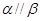 ;
;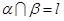 ,若
,若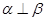 ;
;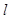 与平面
与平面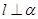 .
.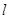 外两点作与直线
外两点作与直线