题目内容
若△ABC的面积为
，BC=1，C=60°，则边AB的长度是（ ）
| 3 |
A、
| ||||
| B、2 | ||||
C、
| ||||
D、
|
考点：正弦定理
专题：解三角形
分析：先利用三角形面积公式求得AC，进而根据余弦定理公式求得AB的值．
解答：
解：S=
AC•BC•sinC=
•AC•1×
=
，
∴AC=4，
∴AB=
=
=
，
故选D．
| 1 |
| 2 |
| 1 |
| 2 |
| ||
| 2 |
| 3 |
∴AC=4，
∴AB=
| AC2+BC2-2AC•BCcos60° |
| 16+1-1×4 |
| 13 |
故选D．
点评：本题主要考查了正弦定理和余弦定理的应用，要求学生对正弦定理和余弦定理公式及变形公式熟练记忆．
练习册系列答案
备战中考寒假系列答案
相关题目
已知平面向量
=（1，2），
=（-3，x），若
∥
，则x等于（ ）
| a |
| b |
| a |
| b |
| A、2 | B、-3 | C、6 | D、-6 |
sin240°=（ ）
A、-
| ||||
| B、-1 | ||||
| C、-2 | ||||
| D、1 |
在等差数列{an}的前n项和为Sn，a2+a3+a4=9，则S5等于（ ）
| A、10 | B、12 | C、15 | D、30 |
给出一个算法的程序框图（如图所示），该程序框图的功能是（ ）
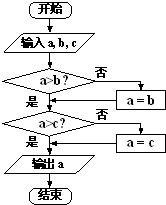
| A、求输出a，b，c三数的最大数 |
| B、求输出a，b，c三数的最小数 |
| C、将a，b，c按从小到大排列 |
| D、将a，b，c按从大到小排列 |
已知在△ABC中，a=
，b=
，B=60°，那么角C等于（ ）
| 2 |
| 3 |
| A、135° | B、90° |
| C、45° | D、75° |
为了得到函数y=sin3x+cos3x的图象，可以将函数y=
sin3x的图象（ ）
| 2 |
A、向右平移
| ||
B、向左平移
| ||
C、向右平移
| ||
D、向左平移
|