题目内容
设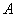 是由
是由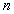 个有序实数构成的一个数组,记作:
个有序实数构成的一个数组,记作: .其中
.其中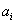
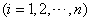 称为数组
称为数组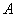 的“元”,
的“元”,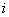 称为
称为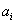 的下标. 如果数组
的下标. 如果数组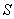 中的每个“元”都是来自 数组
中的每个“元”都是来自 数组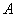 中不同下标的“元”,则称
中不同下标的“元”,则称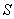 为
为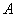 的子数组. 定义两个数组
的子数组. 定义两个数组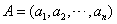 ,
,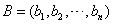 的关系数为
的关系数为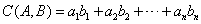 .
.
(Ⅰ)若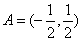 ,
,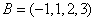 ,设
,设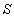 是
是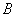 的含有两个“元”的子数组,求
的含有两个“元”的子数组,求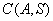 的最大值;
的最大值;
(Ⅱ)若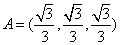 ,
,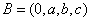 ,且
,且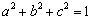 ,
,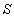 为
为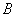 的含有三个“元”的子数组,求
的含有三个“元”的子数组,求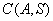 的最大值.
的最大值.
解:(Ⅰ)依据题意,当 时,
时,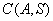 取得最大值为2.
取得最大值为2.
(Ⅱ)①当 是
是 中的“元”时,由于
中的“元”时,由于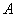 的三个“元”都相等,及
的三个“元”都相等,及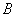 中
中 三个“元”的对称性,可以只计算
三个“元”的对称性,可以只计算 的最大值,其中
的最大值,其中 .
.
由 ,
,
得  .
.
当且仅当 ,且
,且 时,
时, 达到最大值
达到最大值 ,
,
于是 .
.
②当 不是
不是 中的“元”时,计算
中的“元”时,计算 的最大值,
的最大值,
由于 ,
,
所以 .
.
 ,
,
当且仅当 时,等号成立.
时,等号成立.
即当 时,
时, 取得最大值
取得最大值 ,此时
,此时 .
.
综上所述,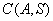 的最大值为1.
的最大值为1.

练习册系列答案
相关题目
 的首项为8,
的首项为8, 是其前n项的和,某同学经计算得S2=20,S3=36,S4=65,后来该同学发现了其中一个数算错了,则该数为 ( )
是其前n项的和,某同学经计算得S2=20,S3=36,S4=65,后来该同学发现了其中一个数算错了,则该数为 ( ) 与圆
与圆 (
( 为参数)相交于
为参数)相交于 ,
, 两点,且弦
两点,且弦 的中点坐标是
的中点坐标是 ,则直线
,则直线 上的函数
上的函数 的对称轴为
的对称轴为 ,且当
,且当 时,
时, .若函数
.若函数 (
( )上有零点,则
)上有零点,则 的值为
的值为 或
或 (B)
(B) (C)
(C) 或
或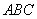 中,三个内角
中,三个内角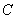 的对边分别为
的对边分别为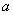 ,
,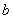 ,
,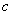 ,且
,且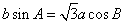 .
.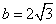 ,求
,求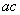 的最大值.
的最大值. 中,
中, ,则
,则
 的解集是 .
的解集是 . 是虚数单位,那么
是虚数单位,那么 等于 .
等于 . 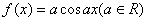 .则下列图象可能为
.则下列图象可能为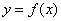 的图象是( )
的图象是( )