题目内容
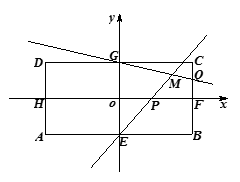
如图,在矩形 中,
中,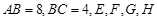 分别为四边的中点,且都在坐标轴上,设
分别为四边的中点,且都在坐标轴上,设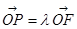 ,
,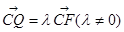 .
.
(Ⅰ)求直线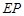 与
与 的交点
的交点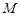 的轨迹
的轨迹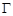 的方程;
的方程;
(Ⅱ)过圆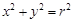
 上一点
上一点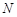 作圆的切线与轨迹
作圆的切线与轨迹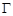 交于
交于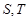 两点,若
两点,若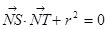 ,试求出
,试求出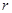 的值.
的值.
(1)
(2)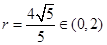
解析试题分析:解:(I)设 ,由已知得
,由已知得 ,
,
则直线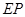 的方程为
的方程为 ,直线
,直线 的方程为
的方程为 , 4分
, 4分
消去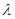 即得
即得 的轨迹
的轨迹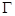 的方程为
的方程为 . 6分
. 6分
(II)方法一:由已知得 ,又
,又 ,则
,则 , 8分
, 8分
设直线 代入
代入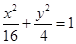 得
得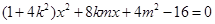 ,
,
设 ,
,
则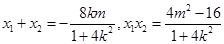 .…10分
.…10分
由 得
得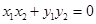 ,
,
即 ,
,
则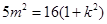 , 12分
, 12分
又 到直线
到直线 的距离为
的距离为 ,故
,故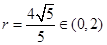 .
.
经检验当直线 的斜率不存在时也满足. 14分
的斜率不存在时也满足. 14分
方法二:设 ,则
,则 ,且可得直线
,且可得直线 的方程为
的方程为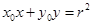 …10分
…10分
代入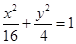 得
得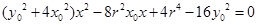 ,
,
由 得
得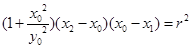 ,即
,即 ,…12分
,…12分
则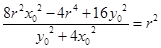 ,故
,故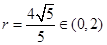 . 14分
. 14分
考点:椭圆方程
点评:主要是考查了直线与椭圆的位置关系的运用,运用代数的方法来解决几何问题,属于中档题。

练习册系列答案
 能考试期末冲刺卷系列答案
能考试期末冲刺卷系列答案
相关题目
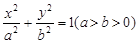 的左、右焦点分别为F1、F2,上顶点为A,△AF1F2为正三角形,且以线段F1F2为直径的圆与直线
的左、右焦点分别为F1、F2,上顶点为A,△AF1F2为正三角形,且以线段F1F2为直径的圆与直线 相切.
相切.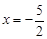 的对称点,动点M满足
的对称点,动点M满足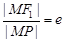 . 问是否存在一个定点T,使得动点M到定点T的距离为定值?若存在,求出定点T的坐标及此定值;若不存在,请说明理由.
. 问是否存在一个定点T,使得动点M到定点T的距离为定值?若存在,求出定点T的坐标及此定值;若不存在,请说明理由. 中,已知椭圆
中,已知椭圆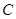 的中心在原点
的中心在原点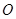 ,焦点在
,焦点在 轴上,短轴长为
轴上,短轴长为 ,离心率为
,离心率为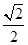 .
.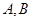 为椭圆
为椭圆 的面积为
的面积为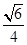 的任意两点,
的任意两点,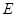 为线段
为线段 的中点,射线
的中点,射线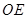 交椭圆
交椭圆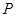 ,设
,设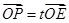 ,求实数
,求实数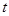 的值.
的值.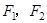 分别是椭圆:
分别是椭圆: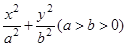 的左、右焦点,过
的左、右焦点,过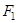 倾斜角为
倾斜角为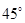 的直线
的直线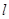 与该椭圆相交于P,
与该椭圆相交于P,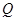 两点,且
两点,且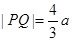 .
.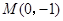 满足
满足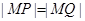 ,求该椭圆的方程.
,求该椭圆的方程.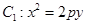 的焦点在抛物线
的焦点在抛物线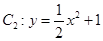 上.
上.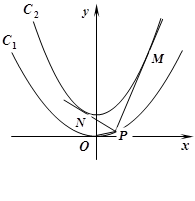
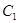 的方程及其准线方程;
的方程及其准线方程;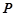 作抛物线
作抛物线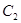 的两条切线
的两条切线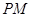 、
、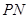 , 切点为
, 切点为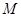 、
、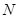 .若
.若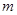 ,且
,且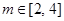 ,求
,求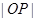 的取值范围.
的取值范围. :
: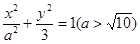 的右焦点
的右焦点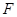 在圆
在圆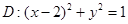 上,直线
上,直线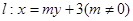 交椭圆于
交椭圆于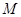 、
、 两点.
两点.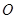 为坐标原点),求
为坐标原点),求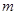 的值;
的值; 设点
设点 轴的对称点为
轴的对称点为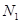 (
( ,试问
,试问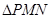 的面积是否存在最大值?若存在,求出这个最大值;若不存在,请说明理由.
的面积是否存在最大值?若存在,求出这个最大值;若不存在,请说明理由.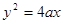 (
(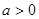 且
且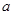 为常数),
为常数),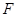 为其焦点.
为其焦点.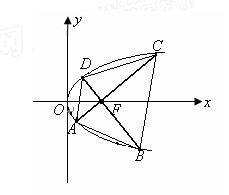
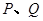 两点,且
两点,且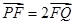 ,求直线
,求直线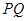 的斜率;
的斜率;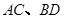 是过抛物线焦点
是过抛物线焦点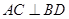 ,如图所示.求四边形
,如图所示.求四边形 面积的最小值
面积的最小值 .
. :
: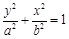
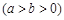 过点
过点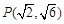 ,上、下焦点分别为
,上、下焦点分别为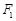 、
、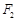 ,
,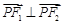 .直线
.直线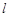 与椭圆交于
与椭圆交于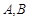 两点,线段
两点,线段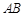 中点为
中点为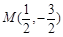 .
.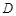 ,若曲线
,若曲线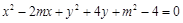 与区域
与区域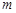 的最小值.
的最小值. ,
,
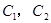 的方程为普通方程,并说明它们分别表示什么曲线?
的方程为普通方程,并说明它们分别表示什么曲线?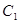 上的点P对应的参数为
上的点P对应的参数为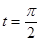 ,Q为
,Q为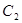 上的动点,求PQ的中点M到直线
上的动点,求PQ的中点M到直线 的距离的最小值
的距离的最小值