题目内容
已知椭圆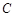 :
: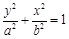
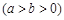 过点
过点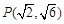 ,上、下焦点分别为
,上、下焦点分别为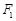 、
、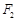 ,
,
向量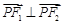 .直线
.直线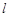 与椭圆交于
与椭圆交于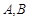 两点,线段
两点,线段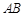 中点为
中点为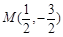 .
.
(1)求椭圆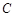 的方程;
的方程;
(2)求直线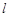 的方程;
的方程;
(3)记椭圆在直线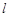 下方的部分与线段
下方的部分与线段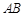 所围成的平面区域(含边界)为
所围成的平面区域(含边界)为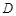 ,若曲线
,若曲线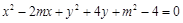 与区域
与区域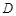 有公共点,试求
有公共点,试求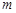 的最小值.
的最小值.
(1)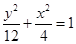 (2)
(2)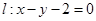 (3)
(3)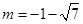
解析试题分析:[解](1)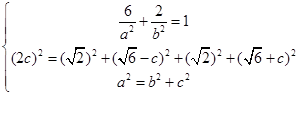
解得: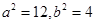 ,椭圆方程为
,椭圆方程为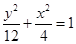
(2)①当斜率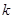 不存在时,由于点
不存在时,由于点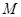 不是线段
不是线段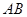 的中点,所以不符合要求;
的中点,所以不符合要求;
②设直线 方程为
方程为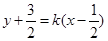 ,代入椭圆方程整理得
,代入椭圆方程整理得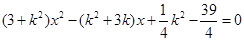
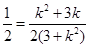
解得
所以直线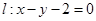
(3)化简曲线方程得: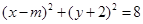 ,是以
,是以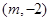 为圆心,
为圆心,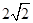 为半径的圆。当圆与直线相切时,
为半径的圆。当圆与直线相切时,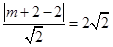 ,此时为
,此时为 ,圆心
,圆心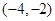 。
。
由于直线与椭圆交于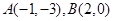 ,
,
故当圆过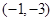 时,
时,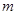 最小。此时,
最小。此时,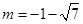 。
。
考点:椭圆的方程
点评:关于曲线的大题,第一问一般是求出曲线的方程,第二问常与直线结合起来,当涉及到交点时,常用到根与系数的关系式: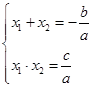 (
(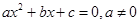 )。
)。

练习册系列答案
 新活力总动员暑系列答案
新活力总动员暑系列答案 龙人图书快乐假期暑假作业郑州大学出版社系列答案
龙人图书快乐假期暑假作业郑州大学出版社系列答案
相关题目
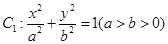 与直线
与直线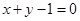 相交于
相交于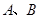 两点.
两点.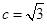 ,直线
,直线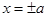 与
与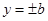 围成的矩形
围成的矩形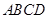 的面积为8,
的面积为8,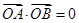 (
(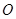 为坐标原点),求证:
为坐标原点),求证: ;
;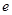 满足
满足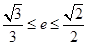 ,求椭圆长轴长的取值范围.
,求椭圆长轴长的取值范围. 中,
中,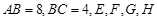 分别为四边的中点,且都在坐标轴上,设
分别为四边的中点,且都在坐标轴上,设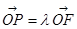 ,
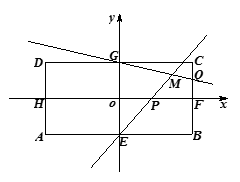
,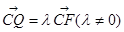 .
.
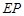 与
与 的交点
的交点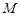 的轨迹
的轨迹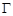 的方程;
的方程;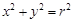
 上一点
上一点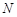 作圆的切线与轨迹
作圆的切线与轨迹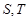 两点,若
两点,若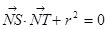 ,试求出
,试求出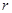 的值.
的值.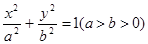 的左焦点为
的左焦点为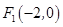 ,直线
,直线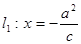 与
与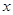 轴交于点
轴交于点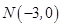 ,过点
,过点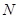 且倾斜角为30°的直线
且倾斜角为30°的直线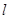 交椭圆于
交椭圆于 两点.
两点. 在以线段
在以线段 为直径的圆上;
为直径的圆上;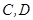 ,以
,以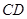 为直径且过点
为直径且过点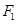 的所有圆中,求面积最小的圆的半径长.
的所有圆中,求面积最小的圆的半径长.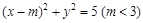 与椭圆E:
与椭圆E: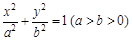 有一个公共点A(3,1),F1、F2分别是椭圆的左、右焦点,直线PF1与圆C相切.
有一个公共点A(3,1),F1、F2分别是椭圆的左、右焦点,直线PF1与圆C相切.
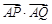 的取值范围.
的取值范围.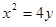 相切于点P(2,1),且与x轴交于点A,定点B(2,0).
相切于点P(2,1),且与x轴交于点A,定点B(2,0).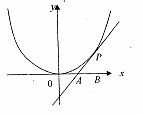
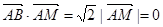 ,求点M轨迹C的方程:
,求点M轨迹C的方程: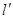 (斜率不为零)与(1)中的轨迹C交于不同的两点E,F(E在B、F之间),试求△OBE与△OBF面积之比的取值范围.
(斜率不为零)与(1)中的轨迹C交于不同的两点E,F(E在B、F之间),试求△OBE与△OBF面积之比的取值范围.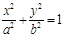 (
(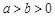 )经过
)经过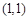 与
与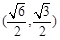 两点.
两点.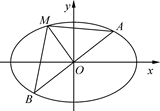
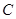 的方程;
的方程;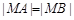 .求证:
.求证: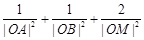 为定值.
为定值.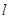 的参数方程为
的参数方程为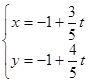 (
(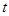 为参数).若以坐标原点O为极点,x轴正半轴为极轴建立极坐标系,则曲线C的极坐标方程为
为参数).若以坐标原点O为极点,x轴正半轴为极轴建立极坐标系,则曲线C的极坐标方程为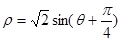 .
.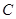 所截得的弦长.
所截得的弦长.