题目内容
已知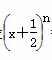
的展开式中前三项的系数成等差数列．设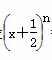＝a0＋a1x＋a2x2＋…＋anxn.求：
(1) a5的值；
(2) a0－a1＋a2－a3＋…＋(－1)nan的值；
(3) ai(i＝0，1，2，…，n)的最大值．
解：(1) 由题设，得
即n2－9n＋8＝0，解得n＝8，n＝1(舍)．
Tr＋1＝C
x8－r
，
令8－r＝5r＝3，所以a5＝7.
(2) 在等式的两边取x＝－1，得a0－a1＋a2－a3＋…＋a8＝
.
(3) 设第r＋1的系数最大，则
即
解得r＝2或r＝3.
所以ai系数最大值为7.
练习册系列答案
相关题目
)图象上一动点，记m＝
，则当m最小时，点P的坐标为________．
的展开式中，第四项和第七项的二项式系数相等，求：
展开式中所有的有理项．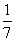
，现有甲、乙两人从袋中轮流摸取1球，甲先取，乙后取，然后甲再取，…，取后不放回，直到两人中有一人取到白球时即终止，每个球在每一次被取出的机会是等可能的，用ξ表示取球终止所需要的取球次数．
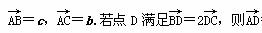＝________．(用b、c表示)