Question

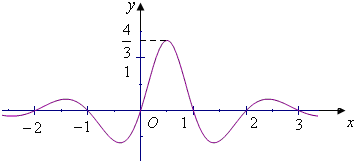如图是函数f(x)=

sinπx

x2-bx+c

的图象的一部分，若图象的最高点的纵坐标为

4

3

，则b+c=

 

．

Answer 1

分析：根据函数f(x)=

sinπx

x2-bx+c

的最高点的纵坐标为

4

3

，从而y=x²-bx+c在x=

1

2

处取最小值

3

4

，建立a、b的等量关系，解之即可，从而求出所求．

解答：解：∵函数f(x)=

sinπx

x2-bx+c

的最高点的纵坐标为

4

3

，
∴y=x²-bx+c在x=

1

2

处取最小值

3

4

即

b 2 = 1 2 1 4 - b 2 +c= 3 4

解得b=c=1
∴b+c=2
故答案为：2

点评：本题主要考查了根据函数的图象求函数的解析式，解题的关键就是抓住最高点进行求解，属于基础题．