题目内容
12.已知函数f(x)=lg$\frac{x+5}{x-5}$.①求f(x)的定义域;
②判断f(x)的奇偶性;
③求f-1(x);
④求使f(x)>0的x的取值范围.
分析 (1)利用对数定义得出$\frac{x+5}{x-5}$>0求解,
(2)根据求函数定义判断.
(3)利用反函数定义求解得出${10^y}=\frac{x+5}{x-5}$∴${f^{-1}}(x)=\frac{{5({{10}^x}+1)}}{{{{10}^x}-1}}(x≠0)$
(4)根据函数单调性转化为不等式求解,注意定义域的限制.
解答 解:(1)∵$\frac{x+5}{x-5}>0$∴定义域为{x|x>5或x<-5};
(2)$f(-x)=lg\frac{-x+5}{-x-5}=lg\frac{x-5}{x+5}=lg{(\frac{x+5}{x-5})^{-1}}=-lg\frac{x+5}{x-5}=-f(x)$
∴f(x)为奇函数;
(3)∵${10^y}=\frac{x+5}{x-5}$∴${f^{-1}}(x)=\frac{{5({{10}^x}+1)}}{{{{10}^x}-1}}(x≠0)$
(4)f(x)>0,
$\frac{x+5}{x-5}$>0∴定义域为{x|x>5或x<-5}
∴$\frac{x+5}{x-5}$>1,解得x>5.
∴x>5
点评 本题综合考察了对数函数的定义,单调性,不等式的运用,属于较简单的综合题目.

练习册系列答案
 芝麻开花课程新体验系列答案
芝麻开花课程新体验系列答案 怎样学好牛津英语系列答案
怎样学好牛津英语系列答案
相关题目
11.下列说法正确的是( )
| A. | 0∉N | B. | $\sqrt{2}$∈Q | C. | π∉R | D. | $\sqrt{4}$∈Z |
17.已知x0(x0>1)是函数f(x)=lnx-$\frac{1}{x-1}$的一个零点,若a∈(1,x0),b∈(x0,+∞),则( )
| A. | f(a)<0,f(b)<0 | B. | f(a)>0,f(b)>0 | C. | f(a)<0,f(b)>0 | D. | f(a)>0,f(b)<0 |
4.某地区在对人们休闲方式的一次调查中,共调查了120人,其中女性70人,男性50人.女性中有40人主要的休闲方式是看电视,另外30人主要的休闲方式是运动;男性中有20人主要的休闲方式是看电视,另外30人主要的休闲方式是运动.
(1)根据以上数据建立一个2×2列联表;
(2)能否在犯错误的概率不超过0.025的前提下认为“性别与休闲方式有关系”?
附:${K^2}=\frac{{n{{(ad-bc)}^2}}}{(a+b)(c+d)(a+c)(b+d)}$
(1)根据以上数据建立一个2×2列联表;
(2)能否在犯错误的概率不超过0.025的前提下认为“性别与休闲方式有关系”?
附:${K^2}=\frac{{n{{(ad-bc)}^2}}}{(a+b)(c+d)(a+c)(b+d)}$
| P(K2≥k) | 0.10 | 0.050 | 0.025 | 0.010 | 0.005 | 0.001 |
| k | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
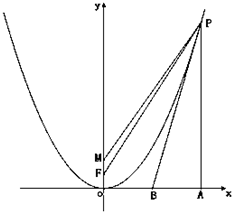 已知点P(x0,y0)(x0≠0)是抛物线x2=2y上的一动点,F为焦点,点M的坐标为(0,1).
已知点P(x0,y0)(x0≠0)是抛物线x2=2y上的一动点,F为焦点,点M的坐标为(0,1).