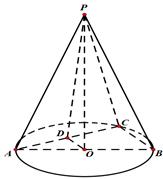
题目内容
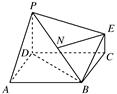
在圆锥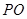 中,已知
中,已知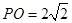 ,
, 的直径
的直径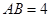 ,点
,点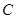 在底面圆周上,且
在底面圆周上,且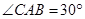 ,
,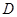 为
为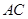 的中点.
的中点.
(1)证明: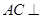 平面
平面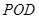 ;
;
(2)求点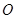 到面
到面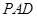 的距离.
的距离.
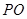 中,已知
中,已知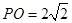 ,
,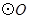 的直径
的直径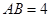 ,点
,点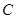 在底面圆周上,且
在底面圆周上,且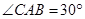 ,
,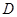 为
为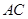 的中点.
的中点.
(1)证明:
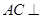 平面
平面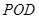 ;
;(2)求点
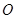 到面
到面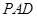 的距离.
的距离.(1)证明详见解析;(2) .
.
 .
.试题分析:(1)先证
 ,再由线面垂直的判定定理证明
,再由线面垂直的判定定理证明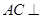 平面
平面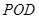 ;(2)作
;(2)作 ,垂足为
,垂足为 ,可证
,可证 平面
平面 ,在
,在 中,利用等面积法可求
中,利用等面积法可求 .
.试题解析:(1)证明:

 面
面 ,且
,且 面
面

 2分
2分由于
 是直径,且点
是直径,且点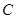 在圆周上,故有
在圆周上,故有
 点
点 分别是
分别是 的中点
的中点 ∥
∥
 5分
5分又

 面
面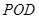 7分
7分(2)由(1)知
 面
面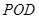 ,又有
,又有 面
面
 面
面 面
面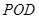 9分
9分 面
面 面
面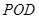 =
=
作
 ,垂足为
,垂足为 ,则有
,则有 面
面
从而
 面
面 11分
11分在
 中,
中,
 13分
13分 14分
14分
练习册系列答案
相关题目

 中,底面
中,底面 为矩形,
为矩形, 平面
平面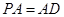 ,
,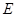 为
为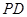 中点.
中点.
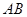 //平面
//平面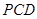 ;
;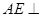 平面
平面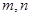 是两条不同的直线,
是两条不同的直线,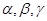 是三个不同的平面,则下列命题中正确命题是( )
是三个不同的平面,则下列命题中正确命题是( )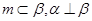 ,则
,则
 ,
,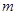 ∥
∥ ,则
,则 ∥
∥
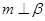 ,
,
 则
则
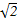 ,E,F分别是BC,AA1的中点.
,E,F分别是BC,AA1的中点.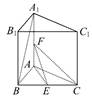
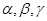 为两两不重合的平面,
为两两不重合的平面,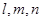 为两两不重合的直线,给出下列四个命题:
为两两不重合的直线,给出下列四个命题: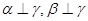 ,则
,则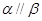 ;
;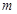
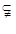
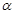 ,
,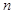
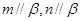 ,则
,则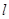
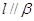 ;
;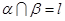 ,
,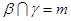 ,
,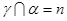 ,
,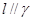 ,则
,则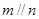 .
.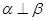 ,
,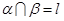 ,直线
,直线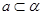 ,直线
,直线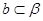 ,
,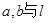 斜交,则( )
斜交,则( )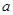 和
和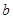 不垂直但可能平行
不垂直但可能平行