题目内容
11.设数列{an}的通项公式为${a_n}={(\frac{3}{2})^{n-1}}$,则满足不等式$\sum_{i=1}^n{\frac{3}{a_i}}>\sum_{i=1}^n{a_i}$的正整数n的集合为{1,2,3}.分析 由等比数列的前n项和公式,可得$9[1-{(\frac{2}{3})}^{n}]$>$2[{(\frac{3}{2})}^{n}-1]$,结合指数的运算性质,可得${(\frac{3}{2})}^{n}$<$\frac{9}{2}$,解得答案.
解答 解:∵${a_n}={(\frac{3}{2})^{n-1}}$,
∴$\sum _{i=1}^{n}\frac{3}{{a}_{i}}$=$\frac{3[1-(\frac{2}{3})^{n}]}{1-\frac{2}{3}}$=$9[1-{(\frac{2}{3})}^{n}]$,$\sum _{i=1}^{n}{a}_{i}=\frac{1-(\frac{3}{2})^{n}}{1-\frac{3}{2}}$=$2[{(\frac{3}{2})}^{n}-1]$,
若$\sum_{i=1}^n{\frac{3}{a_i}}>\sum_{i=1}^n{a_i}$,则$9[1-{(\frac{2}{3})}^{n}]$>$2[{(\frac{3}{2})}^{n}-1]$,
∴$\frac{{(\frac{3}{2})}^{n}-1}{1-{(\frac{2}{3})}^{n}}$=${(\frac{3}{2})}^{n}$<$\frac{9}{2}$,
解得:m=1,n=2,n=3,
∴满足不等式$\sum_{i=1}^n{\frac{3}{a_i}}>\sum_{i=1}^n{a_i}$的正整数n的集合为{1,2,3},
故答案为:{1,2,3}
点评 本题考查的知识点是等比数列的前n项和公式,指数不等式的解法,难度中档.

练习册系列答案
 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案
相关题目
2.设集合A={(x,y)|x+y=1},B={(x,y)|2x-y=-4},则A∩B=( )
| A. | {x=-1,y=2} | B. | (-1,2) | C. | {-1,2} | D. | {(-1,2)} |
16.已知m,n是两条不同的直线,α,β,γ是三个不同的平面,则下列命题中正确的是( )
| A. | 若α⊥γ,α⊥β,则γ∥β | B. | 若m∥n,m?α,n?β,则α∥β | ||
| C. | 若m∥n,m⊥α,n⊥β,则α∥β | D. | 若m∥n,m∥α,则n∥α |
3.已知甲圆锥的半径是乙圆锥半径的3倍,它的高只有乙圆锥高的$\frac{1}{3}$,则甲圆锥与乙圆锥的体积之比为( )
| A. | 1:1 | B. | 3:1 | C. | 9:1 | D. | 1:9 |
20.若不等式-2x2+bx+1>0的解集$\{x|-\frac{1}{2}<x<m\}$,则b,m值是( )
| A. | 1,1 | B. | 1,-1 | C. | -1,1 | D. | -1,-1 |
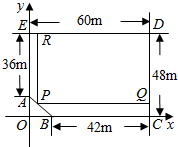 某房地产公司要在荒地ABCDE上划出一块矩形地面DRPQ建造一幢公寓.
某房地产公司要在荒地ABCDE上划出一块矩形地面DRPQ建造一幢公寓.