题目内容
已知椭圆C: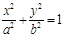 (
(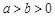 )经过
)经过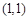 与
与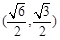 两点.
两点.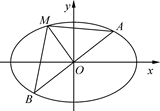
(Ⅰ)求椭圆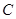 的方程;
的方程;
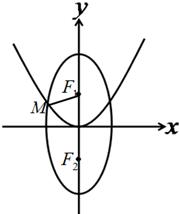
(Ⅱ)过原点的直线l与椭圆C交于A、B两点,椭圆C上一点M满足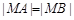 .求证:
.求证: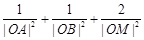 为定值.
为定值.
(Ⅰ)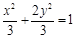 (Ⅱ)①若点A、B是椭圆的短轴顶点,则点M是椭圆的一个长轴顶点,此时
(Ⅱ)①若点A、B是椭圆的短轴顶点,则点M是椭圆的一个长轴顶点,此时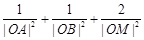
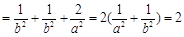 .同理,若点A、B是椭圆的长轴顶点,则点M在椭圆的一个短轴顶点,此时
.同理,若点A、B是椭圆的长轴顶点,则点M在椭圆的一个短轴顶点,此时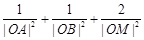
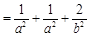
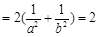 .②若点A、B、M不是椭圆的顶点,设直线l的方程为
.②若点A、B、M不是椭圆的顶点,设直线l的方程为 (
( ),
),
则直线OM的方程为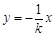 ,设
,设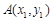 ,
, ,由
,由 解得
解得 ,
, ,∴
,∴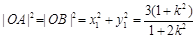 ,同理
,同理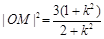 ,所以
,所以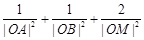
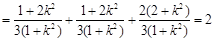 ,
,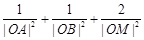 为定值
为定值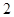 . 13分
. 13分
解析试题分析:(Ⅰ)将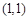 与
与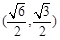 代入椭圆C的方程,
代入椭圆C的方程,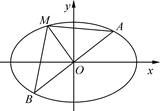
得 解得
解得 ,
,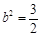 .
.
∴椭圆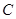 的方程为
的方程为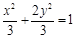 . 6分
. 6分
(Ⅱ)由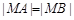 ,知M在线段AB的垂直平分线上,由椭圆的对称性知A、B关于原点对称.
,知M在线段AB的垂直平分线上,由椭圆的对称性知A、B关于原点对称.
①若点A、B是椭圆的短轴顶点,则点M是椭圆的一个长轴顶点,此时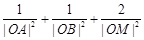
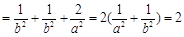 .
.
同理,若点A、B是椭圆的长轴顶点,则点M在椭圆的一个短轴顶点,此时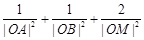
 .
.
②若点A、B、M不是椭圆的顶点,设直线l的方程为 (
( ),
),
则直线OM的方程为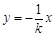 ,设
,设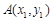 ,
, ,
,
由 解得
解得 ,
, ,
,
∴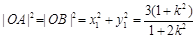 ,同理
,同理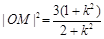 ,
,
所以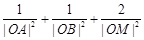
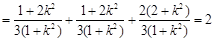 ,
,
故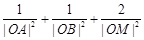 为定值
为定值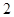 . 13分
. 13分
考点:椭圆方程及直线与椭圆的位置关系
点评:求椭圆方程采用的待定系数法,第二问中要证明式子结果是定值首先需求出点 坐标,结合已知条件可知这三点坐标教容易求出,因此只需联立方程求解即可
坐标,结合已知条件可知这三点坐标教容易求出,因此只需联立方程求解即可

练习册系列答案
 倍速训练法直通中考考点系列答案
倍速训练法直通中考考点系列答案 一卷搞定系列答案
一卷搞定系列答案 名校作业本系列答案
名校作业本系列答案 轻巧夺冠周测月考直通名校系列答案
轻巧夺冠周测月考直通名校系列答案
相关题目
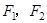 分别是椭圆:
分别是椭圆: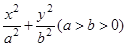 的左、右焦点,过
的左、右焦点,过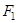 倾斜角为
倾斜角为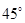 的直线
的直线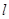 与该椭圆相交于P,
与该椭圆相交于P,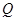 两点,且
两点,且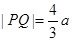 .
.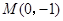 满足
满足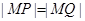 ,求该椭圆的方程.
,求该椭圆的方程.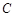 :
: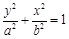
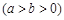 过点
过点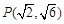 ,上、下焦点分别为
,上、下焦点分别为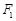 、
、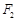 ,
,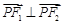 .直线
.直线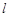 与椭圆交于
与椭圆交于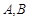 两点,线段
两点,线段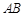 中点为
中点为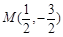 .
.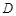 ,若曲线
,若曲线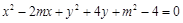 与区域
与区域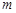 的最小值.
的最小值.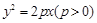 的焦点为
的焦点为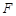 ,点
,点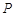 是抛物线上的一点,且其纵坐标为4,
是抛物线上的一点,且其纵坐标为4,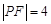 .
.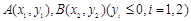 是抛物线上的两点,
是抛物线上的两点,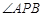 的角平分线与
的角平分线与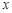 轴垂直,求直线AB的斜率;
轴垂直,求直线AB的斜率;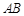 过点
过点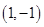 ,求弦
,求弦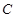 的中心在坐标原点,焦点在
的中心在坐标原点,焦点在 轴上,其左、右焦点分别为
轴上,其左、右焦点分别为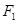 、
、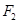 ,短轴长为
,短轴长为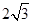 ,点
,点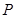 在椭圆
在椭圆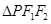 的周长为6.
的周长为6.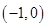 的直线与椭圆相交于A、B两点,试问在x轴上是否存在一个定点M使
的直线与椭圆相交于A、B两点,试问在x轴上是否存在一个定点M使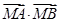 恒为定值?若存在求出该定值及点M的坐标,若不存在请说明理由.
恒为定值?若存在求出该定值及点M的坐标,若不存在请说明理由.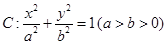 .
.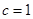 ,且
,且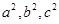 成等差数列,求椭圆
成等差数列,求椭圆 的方程;
的方程;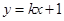 相交于
相交于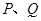 两点,求
两点,求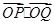 的取值范围.
的取值范围. ,
,
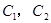 的方程为普通方程,并说明它们分别表示什么曲线?
的方程为普通方程,并说明它们分别表示什么曲线?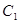 上的点P对应的参数为
上的点P对应的参数为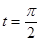 ,Q为
,Q为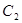 上的动点,求PQ的中点M到直线
上的动点,求PQ的中点M到直线 的距离的最小值
的距离的最小值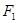 、
、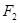 分别为椭圆
分别为椭圆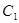 :
: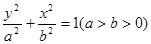 的上、下焦点,其中
的上、下焦点,其中 :
: 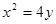 的焦点,点
的焦点,点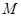 是
是 。
。
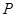 (1,3)和圆
(1,3)和圆 :
: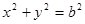 ,过点
,过点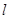 与圆
与圆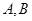 ,在线段
,在线段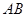 取一点
取一点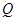 ,满足:
,满足: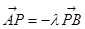 ,
,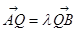 (
(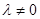 且
且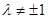 )。
)。 的离心率为
的离心率为 ,右准线方程为
,右准线方程为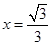 。
。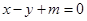 与双曲线C交于不同的两点A,B,且线段AB的中点在圆
与双曲线C交于不同的两点A,B,且线段AB的中点在圆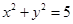 上,求实数m的值。
上,求实数m的值。