题目内容
(本小题满分12分)已知⊙C:x2+y2-2x-2y+1=0,直线l与⊙C相切且分别交x轴、y轴正向于A、B两点,O为坐标原点,且 =a,
=a, =b(a>2,b>2).
=b(a>2,b>2).
(Ⅰ)求线段AB中点的轨迹方程.
(Ⅱ)求△ABC面积的极小值.
解:C:(x-1)2+(y-1)2=1,A(a,O),B(O,b) .设直线AB的方程为
bx+ay-ab=0,∵直线AB与⊙C相切,
∴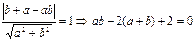 ①…………………………………2分
①…………………………………2分
(Ⅰ)设AB中点P(x,y),则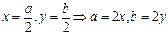 代入
代入 ①得P点的轨迹方程:2xy
①得P点的轨迹方程:2xy
-2x-2y+1=0,∵a>2,∴x> 1.
1.
∴P点的轨迹方程为(x-1)(y-1)=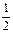 (x>1).
(x>1). …………………………………7分
…………………………………7分
(Ⅱ)由①得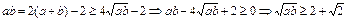 ,当且仅当
,当且仅当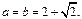 时等号成立.
时等号成立.
S△AOB=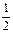 ab≥3+2
ab≥3+2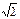 .………………………………12分
.………………………………12分
解析

练习册系列答案
相关题目
.(5分)直线 与曲线
与曲线 有且只有一个交点,则
有且只有一个交点,则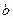 的取值范围是( )
的取值范围是( )
A. | B. 且 且 | C. | D. |
 的圆形村落,
的圆形村落,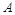 、
、 两人同时从村落中心出发。
两人同时从村落中心出发。 ,且后来
,且后来
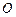 为平面直角坐标系的原点,过点
为平面直角坐标系的原点,过点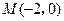 的直线
的直线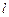 与圆
与圆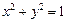 交于
交于 ,
,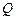 两点.
两点.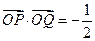 ,求直线
,求直线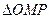 与
与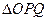 的面积相等,求直线
的面积相等,求直线 相交,所得公共弦平行于已知直线
相交,所得公共弦平行于已知直线 ,又圆C经过点A(-2,3),B(1,4),求圆C的方程。
,又圆C经过点A(-2,3),B(1,4),求圆C的方程。 B = 90°,AC = 4,BC =
B = 90°,AC = 4,BC = 2,点P为线段CA(不包括端点)上的一个动点,以
2,点P为线段CA(不包括端点)上的一个动点,以 为圆心,1为半径作
为圆心,1为半径作 .
. ,若
,若 ,试判断
,试判断
 :
: 和
和 ,动点
,动点 到圆
到圆 |的比等于常数
|的比等于常数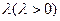 ,求动点
,求动点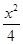 +y2=1的左、右焦点,P是第一象限内该椭圆上的一点,且PF1⊥PF2,则点P的横坐标为( )
+y2=1的左、右焦点,P是第一象限内该椭圆上的一点,且PF1⊥PF2,则点P的横坐标为( )