题目内容
如图，已知三棱锥D-ABC的底面是正三角形，且DA⊥平面ABC，O为底面中心，M、N是BD上的两点，且BM=DM=3MN（1）ON∥平面MAC；
（2）若AM⊥BD，求BO与平面MAC所成角的正弦值．
考点：直线与平面平行的判定,直线与平面所成的角
专题：空间位置关系与距离,空间角
分析：（1）延长BO交AC于E，连接ME，根据重心的几何特征结合已知和平行线分线段成比例定理可得：ON∥ME，再由线面平行的判定定理得到ON∥平面MAC；
（2）若AM⊥BD，可得△ABD，以A为原点建立空间坐标系，求出BO的方向向量和平面MAC的法向量，代入向量夹角公式，可得答案．
（2）若AM⊥BD，可得△ABD，以A为原点建立空间坐标系，求出BO的方向向量和平面MAC的法向量，代入向量夹角公式，可得答案．
解答：
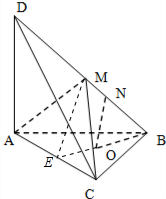证明：（1）延长BO交AC于E，连接ME，
∵O为底面正三角形ABC的中心，
故E为AC的中点，且BO：OE=2：1，
又由BM=DM=3MN，
∴BN：NM=2：1，
故ON∥ME，
又∵ON?平面MAC，ME?平面MAC，
∴ON∥平面MAC；
解：（2）∵DA⊥平面ABC，AB?平面ABC，
∴DA⊥AB，
又∵ABM为BD的中点，AM⊥BD，
故△ABD为等腰直角三角形，
以A为坐标原点，建立如图所示的空间直角坐标系，
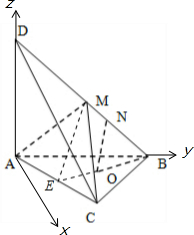
设AD=AB=AC=BC=2a，
则B（0，2a，0），D（0，0，2a），M（0，a，a），C（
a，a，0），O（
，a，0），
则
=（
，-a，0），
=（0，a，a），
=（
a，a，0），
设平面MAC的一个法向量为
=（x，y，z），
则由
得：
，
即
，
令x=1，则
=（1，-
，
）为平面MAC的一个法向量，
设BO与平面MAC所成角为θ，
则sinθ=
=
=
证明：（1）延长BO交AC于E，连接ME，∵O为底面正三角形ABC的中心，
故E为AC的中点，且BO：OE=2：1，
又由BM=DM=3MN，
∴BN：NM=2：1，
故ON∥ME，
又∵ON?平面MAC，ME?平面MAC，
∴ON∥平面MAC；
解：（2）∵DA⊥平面ABC，AB?平面ABC，
∴DA⊥AB，
又∵ABM为BD的中点，AM⊥BD，
故△ABD为等腰直角三角形，
以A为坐标原点，建立如图所示的空间直角坐标系，
设AD=AB=AC=BC=2a，
则B（0，2a，0），D（0，0，2a），M（0，a，a），C（
| 3 |
| ||
| 3 |
则
| BO |
| ||
| 3 |
| AM |
| AC |
| 3 |
设平面MAC的一个法向量为
| m |
则由
|
|
即
|
令x=1，则
| m |
| 3 |
| 3 |
设BO与平面MAC所成角为θ，
则sinθ=
|
| ||||
|
|
| ||||||
|
2
| ||
| 7 |
点评：本题考查的知识点是直线与平面平行的判定，直线与平面所成的角，建立空间坐标系，将空间线面夹角问题，转化为向量夹角问题是解答的关键．
练习册系列答案
相关题目
某县工业园区人才市场举办农民工招聘洽谈活动，某服装厂经过综合测试，录用了14名男工和6名女工，这20名工人的测试成绩如茎叶图所示，服装厂规定：成绩在180分以上者到“甲车间”工作；180分以下者到“乙车间”工作．