题目内容
 右图是一个直三棱柱(以A1B1C1为底面),被一平面所截得的几何体,截面为ABC.已知A1B1=B1C1=1,∠A1B1C1=900,AA1=4,BB1=2,CC1=3
右图是一个直三棱柱(以A1B1C1为底面),被一平面所截得的几何体,截面为ABC.已知A1B1=B1C1=1,∠A1B1C1=900,AA1=4,BB1=2,CC1=3(I)设点O是AB的中点,证明:OC∥平面A1B1C1
(II)求AB与平面AA1CC1所成角的大小.
分析:法一:(1)要证明OC∥平面A1B1C1可利用线面平行的判定定理来证明则可过OD∥AA1交A1B1于D,连C1D则根据直三棱柱的性质和平行的传递性可得OD∥AA1交A1B1于D,并且根据梯形的中位线定理可得OD=
(AA1+BB1)=3=CC1即可得ODC1C是平行四边形故OC∥C1D然后根据线面平行的判定定理即可证明.
(2)过B作截面BA2C2∥面A1B1C1分别交AA1,CC1于A2,C2根据直三棱柱的性质可得面BA2C2⊥面AA1C1C然后根据面面垂直的性质定理和△A1B1C1的特征可得过B作面AA1C1C的垂线这垂足落在A2C2的中点H上则∠BAH就是AB与面AA1C1C所成的角再利用条件解△AHB即可求解.
法二:可利用向量的有关知识来证明.根据题意可建立如图所示的空间直角坐标系.
(1)根据空间直角坐标系可求出
=(1,-
,0)且平面A1B1C1的一个法向量为
=(0,0,1)再根据向量的数量积可得
•
=0即可证明平面A1B1C1知OC∥平面A1B1C1.
(2)求出
=(0,-1,-2),和平面AA1C1C的一个法向量
=(1,1,0)根据响亮的夹角公式可求出,cos<
,
>=
=-
<0故AB与平面AA1CC1所成角θ=<
,
>-
从而求出sinθ=
即θ=arcsin
| 1 |
| 2 |
(2)过B作截面BA2C2∥面A1B1C1分别交AA1,CC1于A2,C2根据直三棱柱的性质可得面BA2C2⊥面AA1C1C然后根据面面垂直的性质定理和△A1B1C1的特征可得过B作面AA1C1C的垂线这垂足落在A2C2的中点H上则∠BAH就是AB与面AA1C1C所成的角再利用条件解△AHB即可求解.
法二:可利用向量的有关知识来证明.根据题意可建立如图所示的空间直角坐标系.
(1)根据空间直角坐标系可求出
| OC |
| 1 |
| 2 |
| n |
| OC |
| n |
(2)求出
| AB |
| m |
| m |
| AB |
| ||||
|
|
| ||
| 10 |
| m |
| AB |
| π |
| 2 |
| ||
| 10 |
| ||
| 10 |
解答: 解:(Ⅰ)证明:作OD∥AA1交A1B1于D,连C1D.
解:(Ⅰ)证明:作OD∥AA1交A1B1于D,连C1D.
则OD∥AA1交A1B1于D,连C1D因为O是AB的中点,
所以OD=
(AA1+BB1)=3=CC1.
则ODC1C是平行四边形,因此有OC∥C1D,C1D?平面C1B1A1,且OC?平面C1B1A1
则OC∥面A1B1C1. ….(7分)
(Ⅱ)解:如图,过B作截面BA2C2∥面A1B1C1,分别交AA1,CC1于A2,C2,
作BH⊥A2C2于H,
因为平面A2BC2⊥平面AA1C1C,则BH⊥面AA1C1C.
连接AH,则∠BAH就是AB与面AA1C1C所成的角.
因为BH=
,AB=
,所以sin∠BAH=
=
.AB与面AA1C1C所成的角为∠BAH=arcsin
.….(14分)
解法二:
(Ⅰ)证明:如图,以B1为原点建立空间直角坐标系,则A(0,1,4),B(0,0,2),C(1,0,3),因为O是AB的中点,所以O(0,
,3),
=(1,-
,0),
易知,
=(0,0,1)是平面A1B1C1的一个法向量.
由
•
=0且OC?平面A1B1C1知OC∥平面A1B1C1.
….(7分)
(Ⅱ)设AB与面AA1C1C所成的角为θ.
求得
=(0,0,4),
=(1,-1,0).
设
=(x,y,z)是平面AA1C1C的一个法向量,则由
得
,
取x=y=1得:
=(1,1,0).
又因为
=(0,-1,-2),,
所以,cos<
,
>=
=-
则sinθ=
.
所以AB与面AA1C1C所成的角为arcsin
.….(14分)
 解:(Ⅰ)证明:作OD∥AA1交A1B1于D,连C1D.
解:(Ⅰ)证明:作OD∥AA1交A1B1于D,连C1D.则OD∥AA1交A1B1于D,连C1D因为O是AB的中点,
所以OD=
| 1 |
| 2 |
则ODC1C是平行四边形,因此有OC∥C1D,C1D?平面C1B1A1,且OC?平面C1B1A1
则OC∥面A1B1C1. ….(7分)
(Ⅱ)解:如图,过B作截面BA2C2∥面A1B1C1,分别交AA1,CC1于A2,C2,
作BH⊥A2C2于H,
因为平面A2BC2⊥平面AA1C1C,则BH⊥面AA1C1C.
连接AH,则∠BAH就是AB与面AA1C1C所成的角.
因为BH=
| ||
| 2 |
| 5 |
| BH |
| AB |
| ||
| 10 |
| ||
| 10 |
解法二:
(Ⅰ)证明:如图,以B1为原点建立空间直角坐标系,则A(0,1,4),B(0,0,2),C(1,0,3),因为O是AB的中点,所以O(0,
| 1 |
| 2 |
| OC |
| 1 |
| 2 |

易知,
| n |
由
| OC |
| n |
….(7分)
(Ⅱ)设AB与面AA1C1C所成的角为θ.
求得
| A1A |
| A1C1 |
设
| m |
|
|
取x=y=1得:
| m |
又因为
| AB |
所以,cos<
| m |
| AB |
| ||||
|
|
| ||
| 10 |
| ||
| 10 |
所以AB与面AA1C1C所成的角为arcsin
| ||
| 10 |
点评:本题主要考查了线面平行的证明和线面角的求解.解题的关键是熟练掌握几何法和向量法是解决此类问题常用的方法!

练习册系列答案
相关题目
 (本小题14分)右图是一个直三棱柱(以
(本小题14分)右图是一个直三棱柱(以 (本小题14分)右图是一个直三棱柱(以
(本小题14分)右图是一个直三棱柱(以 为底面)被一平面所截得到的几何体,截面为
为底面)被一平面所截得到的几何体,截面为 .已知
.已知 ,
, ,
, ,
, ,
, .
.
 是
是 的中点,证明:
的中点,证明: 平面
平面 的大小;
的大小; 为底面)被一平面所截得到的几何体,截面为
为底面)被一平面所截得到的几何体,截面为 已知
已知 ,
, ,
, ,
, ,
,

 是
是 的中点,证明:
的中点,证明: 平面
平面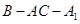 的大小;
的大小;