题目内容
右图是一个直三棱柱(以 为底面)被一平面所截得到的几何体,截面为
为底面)被一平面所截得到的几何体,截面为 .已知
.已知 ,
, ,
, ,
, ,
, .
.

(1)设点 是
是 的中点,证明:
的中点,证明: 平面
平面 ;
;
(2)求二面角 的大小;
的大小;
【答案】
(1)证明见试题解析;(2) .
.
【解析】
试题分析:(1)证线面平行,一般根据线面平行的判定定理,在平面 内找到一条与
内找到一条与 平行的直线即可.为此我们取
平行的直线即可.为此我们取 中点D,证明
中点D,证明 //
//  .(2)要求二面角的大小,一般是先作出二面角的平面角,通过求这个平面角来求出二面角.由于该几何体的三个侧面都是直角梯形,易计算得
.(2)要求二面角的大小,一般是先作出二面角的平面角,通过求这个平面角来求出二面角.由于该几何体的三个侧面都是直角梯形,易计算得 ,
, ,
, ,从而
,从而 ,所以
,所以 。那么二面角的平面角可以直接在平面
。那么二面角的平面角可以直接在平面 内过点
内过点 作
作 ,或者作
,或者作 平面
平面 ,垂足为
,垂足为 ,连接
,连接 ,由三垂线定理知
,由三垂线定理知 ,
, 就是所作平面角。
就是所作平面角。
试题解析:(1)证明:作 交
交 于
于 ,连
,连 .
.
则 .
.
因为 是
是 的中点,
的中点,
所以 .
.
则 是平行四边形,因此有
是平行四边形,因此有 .
.
 平面
平面 且
且 平面
平面 ,
,
则 面
面 .
.
(2)如图,过 作截面
作截面 面
面 ,分别交
,分别交 ,
, 于
于 ,
, .
.

作 于
于 ,连
,连 .
.
因为 面
面 ,所以
,所以 ,则
,则 平面
平面 .
.
又因为 ,
, ,
, .
.
所以 ,根据三垂线定理知
,根据三垂线定理知 ,所以
,所以 就是所求二面角的平面角.
就是所求二面角的平面角.
因为 ,所以
,所以 ,故
,故 ,
,
即:所求二面角的大小为 .
.
考点:(1)线面平行;(2)二面角.

练习册系列答案
相关题目
 右图是一个直三棱柱(以A1B1C1为底面),被一平面所截得的几何体,截面为ABC.已知A1B1=B1C1=1,∠A1B1C1=900,AA1=4,BB1=2,CC1=3
右图是一个直三棱柱(以A1B1C1为底面),被一平面所截得的几何体,截面为ABC.已知A1B1=B1C1=1,∠A1B1C1=900,AA1=4,BB1=2,CC1=3 (本小题14分)右图是一个直三棱柱(以
(本小题14分)右图是一个直三棱柱(以 (本小题14分)右图是一个直三棱柱(以
(本小题14分)右图是一个直三棱柱(以 为底面)被一平面所截得到的几何体,截面为
为底面)被一平面所截得到的几何体,截面为 已知
已知 ,
, ,
, ,
, ,
,

 是
是 的中点,证明:
的中点,证明: 平面
平面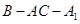 的大小;
的大小;