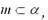题目内容
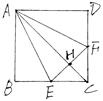
如图,在斜三棱柱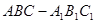 中,点
中,点 、
、 分别是
分别是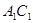 、
、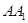 的中点,
的中点,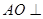 平面
平面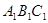 .已知
.已知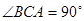 ,
,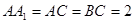 .
.
(Ⅰ)证明: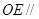 平面
平面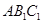 ;
;
(Ⅱ)求异面直线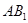 与
与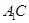 所成的角;
所成的角;
(Ⅲ)求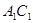 与平面
与平面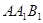 所成角的正弦值.
所成角的正弦值.
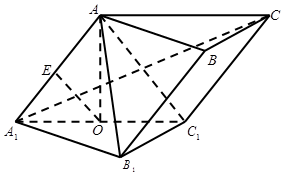
 中,点
中,点 、
、 分别是
分别是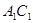 、
、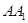 的中点,
的中点,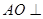 平面
平面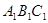 .已知
.已知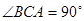 ,
,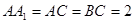 .
.(Ⅰ)证明:
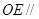 平面
平面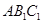 ;
;(Ⅱ)求异面直线
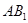 与
与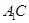 所成的角;
所成的角;(Ⅲ)求
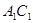 与平面
与平面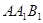 所成角的正弦值.
所成角的正弦值.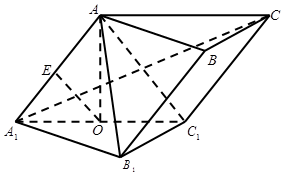
(1)见解析;(2)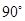 ;(3)
;(3)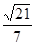 .
.
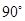 ;(3)
;(3)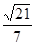 .
.本试题主要考查了立体几何中的线面平行和异面直线所称的角,以及线面角的求解的综合运用,考查了空间想象能力‘
解法一:(Ⅰ)证明:∵点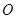 、
、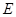 分别是
分别是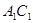 、
、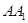 的中点,
的中点,
∴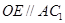 ,又∵
,又∵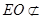 平面
平面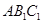 ,
,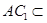 平面
平面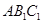 ,
,
∴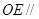 平面
平面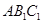 .···························· 4分
.···························· 4分
(Ⅱ)∵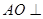 平面
平面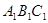 ,∴
,∴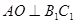 ,又∵
,又∵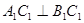 ,且
,且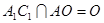 ,
,
∴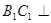 平面
平面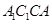 ,∴
,∴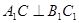 .··················· 6分
.··················· 6分
又∵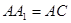 , ∴四边形
, ∴四边形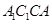 为菱形,
为菱形,
∴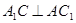 ,且
,且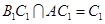 ∴
∴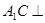 平面
平面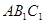 ,
,
∴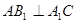 ,即异面直线
,即异面直线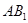 与
与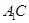 所成的角为
所成的角为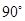 .············· 8分
.············· 8分
(Ⅲ) 设点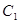 到平面
到平面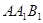 的距离为
的距离为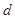 ,∵
,∵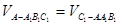 ,
,
即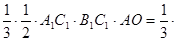
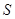 △
△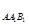
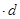 .·················· 10分
.·················· 10分
又∵在△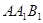 中,
中,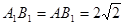 ,∴
,∴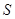 △
△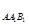
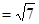 .
.
∴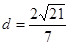 ,∴
,∴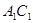 与平面
与平面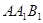 所成角的正弦值
所成角的正弦值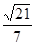 .·········· 12分
.·········· 12分

解法二:如图建系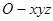 ,
,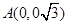 ,
,
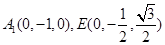 ,
,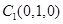 ,
, 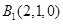 ,
,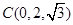 .……………2分
.……………2分
(Ⅰ)∵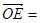
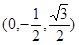 ,
,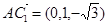 ,∴
,∴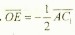 ,,即
,,即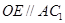 ,
,
又∵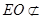 平面
平面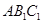 ,
,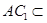 平面
平面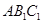 ,∴
,∴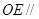 平面
平面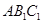 .······· 6分
.······· 6分
(Ⅱ)∵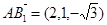 ,
,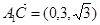 ,∴
,∴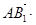
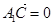 ,即∴
,即∴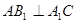 ,
,
∴异面直线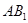 与
与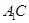 所成的角为
所成的角为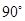 .···················· 8分
.···················· 8分
(Ⅲ)设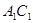 与平面
与平面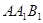 所成角为
所成角为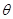 ,∵
,∵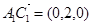 ,
,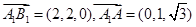
设平面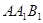 的一个法向量是
的一个法向量是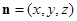
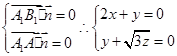
不妨令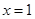 ,可得
,可得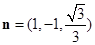 ,····················· 10分
,····················· 10分
∴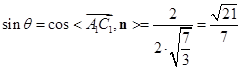 ,∴
,∴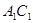 与平面
与平面 所成角的正弦值
所成角的正弦值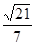 . 12分
. 12分
解法一:(Ⅰ)证明:∵点
 、
、 分别是
分别是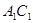 、
、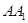 的中点,
的中点,∴
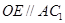 ,又∵
,又∵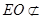 平面
平面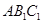 ,
,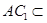 平面
平面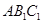 ,
,∴
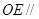 平面
平面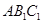 .···························· 4分
.···························· 4分(Ⅱ)∵
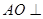 平面
平面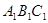 ,∴
,∴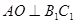 ,又∵
,又∵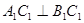 ,且
,且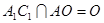 ,
,∴
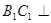 平面
平面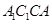 ,∴
,∴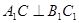 .··················· 6分
.··················· 6分又∵
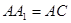 , ∴四边形
, ∴四边形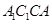 为菱形,
为菱形,∴
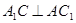 ,且
,且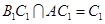 ∴
∴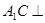 平面
平面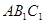 ,
,∴
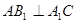 ,即异面直线
,即异面直线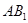 与
与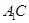 所成的角为
所成的角为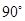 .············· 8分
.············· 8分(Ⅲ) 设点
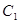 到平面
到平面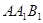 的距离为
的距离为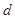 ,∵
,∵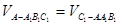 ,
,即
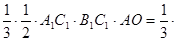
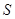 △
△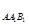
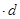 .·················· 10分
.·················· 10分又∵在△
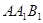 中,
中,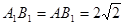 ,∴
,∴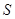 △
△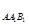
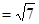 .
.∴
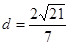 ,∴
,∴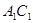 与平面
与平面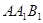 所成角的正弦值
所成角的正弦值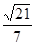 .·········· 12分
.·········· 12分
解法二:如图建系
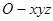 ,
,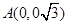 ,
,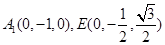 ,
,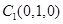 ,
, 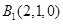 ,
,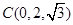 .……………2分
.……………2分(Ⅰ)∵
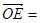
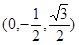 ,
,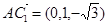 ,∴
,∴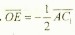 ,,即
,,即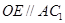 ,
,又∵
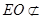 平面
平面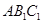 ,
,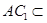 平面
平面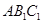 ,∴
,∴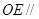 平面
平面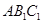 .······· 6分
.······· 6分(Ⅱ)∵
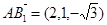 ,
,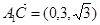 ,∴
,∴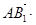
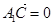 ,即∴
,即∴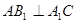 ,
,∴异面直线
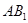 与
与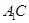 所成的角为
所成的角为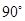 .···················· 8分
.···················· 8分(Ⅲ)设
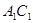 与平面
与平面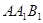 所成角为
所成角为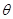 ,∵
,∵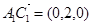 ,
,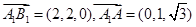
设平面
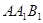 的一个法向量是
的一个法向量是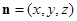
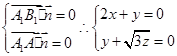
不妨令
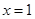 ,可得
,可得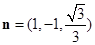 ,····················· 10分
,····················· 10分∴
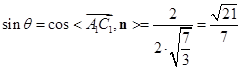 ,∴
,∴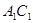 与平面
与平面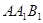 所成角的正弦值
所成角的正弦值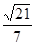 . 12分
. 12分
练习册系列答案
 全优点练单元计划系列答案
全优点练单元计划系列答案
相关题目
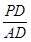 =
=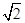 ,求平面PBE与平面ABCD所成的锐二面角的大小.
,求平面PBE与平面ABCD所成的锐二面角的大小.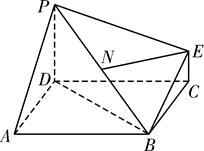
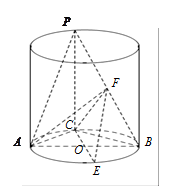
 长度为
长度为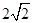 ,
,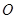 为底面圆心,正三角形
为底面圆心,正三角形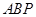 的一个顶点
的一个顶点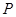 在上底面的圆周上,
在上底面的圆周上,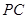 为圆柱的母线,
为圆柱的母线,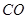 的延长线交
的延长线交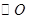 于点
于点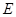 ,
, 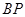 的中点为
的中点为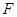 .
.
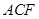 ;
;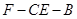 的正切值.
的正切值. 中,
中, ,
, ,点
,点 在棱
在棱 上移动,问
上移动,问 等于何值时,二面角
等于何值时,二面角 的大小为
的大小为 .
.
 平面EFG
平面EFG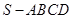 中,
中, 平面
平面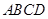 ,底面
,底面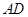 ∥
∥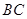 ,
,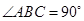 ,
,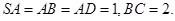
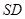 所成角的大小;
所成角的大小;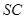 与平面
与平面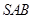 所成角的正切值;
所成角的正切值;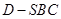 的体积.
的体积.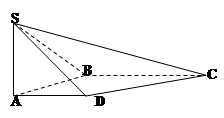
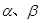 是两个不同的平面,m、n是平面
是两个不同的平面,m、n是平面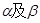 之外的两条不同的直线,给出四个论断: ①m⊥n,②
之外的两条不同的直线,给出四个论断: ①m⊥n,②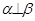 ,③
,③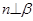 ,④
,④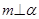 。
。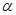 和共面
和共面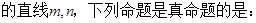 ( )
( )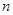
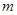 ∥
∥