题目内容
已知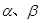 是两个不同的平面,m、n是平面
是两个不同的平面,m、n是平面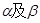 之外的两条不同的直线,给出四个论断: ①m⊥n,②
之外的两条不同的直线,给出四个论断: ①m⊥n,②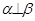 ,③
,③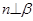 ,④
,④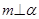 。
。
以其中三个论断作为条件,余下一个论断作为结论,写出你认为正确的一个命题________。
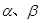 是两个不同的平面,m、n是平面
是两个不同的平面,m、n是平面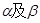 之外的两条不同的直线,给出四个论断: ①m⊥n,②
之外的两条不同的直线,给出四个论断: ①m⊥n,②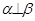 ,③
,③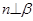 ,④
,④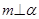 。
。以其中三个论断作为条件,余下一个论断作为结论,写出你认为正确的一个命题________。

 或
或
下证:

∵
 ,∴存在
,∴存在 ,有
,有 共面
共面而
 ,∴
,∴
再由
 ,
, 共面,可得
共面,可得
∵
 ,∴
,∴
而
 ,∴
,∴
下证:

∵
 ,∴存在
,∴存在 ,有
,有
∵
 ,∴
,∴
而
 ,∴
,∴ ,则存在
,则存在 ,有
,有
∵
 ,∴
,∴ ,则
,则

练习册系列答案
相关题目
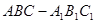 中,点
中,点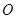 、
、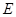 分别是
分别是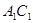 、
、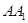 的中点,
的中点,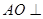 平面
平面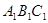 .已知
.已知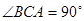 ,
,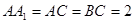 .
.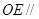 平面
平面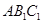 ;
;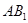 与
与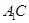 所成的角;
所成的角;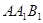 所成角的正弦值.
所成角的正弦值.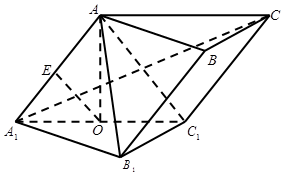
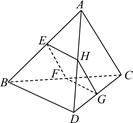
 中,
中, ,点
,点 是
是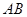 的中点.
的中点.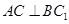 ;(2)
;(2)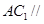 平面
平面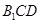 .
.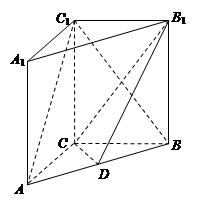
 是平面,
是平面,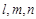 是直线,则下列命题正确的是( )
是直线,则下列命题正确的是( )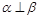 ,
,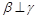 ,则
,则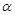 ∥
∥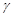
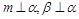 ,则
,则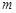 ∥
∥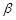
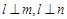 ,则
,则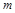 ∥
∥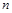
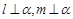 ,则
,则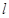 ∥
∥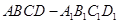 中,E,P分别是侧棱B1C1,
中,E,P分别是侧棱B1C1,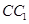 上的中点
上的中点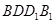 所成角的正切值
所成角的正切值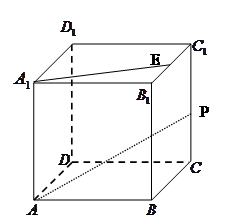
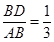
 时,求二面角
时,求二面角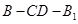 的余弦值.
的余弦值.
 ⊥平面
⊥平面 ,那么平面
,那么平面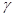 ,平面
,平面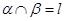 ,那么
,那么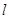 ⊥平面
⊥平面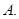 1
1 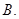 2
2 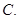 3
3 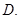 4
4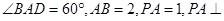 平面ABCD,E是PC的中点,F是AB的中点。
平面ABCD,E是PC的中点,F是AB的中点。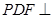 平面PAB;
平面PAB;