题目内容
把数列{
}的所有项按照从大到小,左大右小的原则写成如图所示的数表,第k行有2k-1个数,第k行的第s个数(从左数起)记为(k,s),则
可记为______.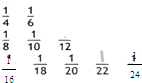
| 1 |
| 2n |
| 1 |
| 8888 |

由第k行有2k-1个数,知每一行数的个数构成等比数列,首项是1,公比是2,
∴前k-1行共有
=2k-1-1个数,
∴第k行第一个数是A(k,1)=
=
,
∴A(k,s)=
,
由
=
,得2k+2s-2=8888,s≤2k-1,
解得k=13,s=175.
则这个数记作A(13,175).
故答案为:(13,175)
∴前k-1行共有
| 1-2k-1 |
| 1-2 |
∴第k行第一个数是A(k,1)=
| 1 |
| 22•k-1 |
| 1 |
| 2k |
∴A(k,s)=
| 1 |
| 2k+2(s-1) |
由
| 1 |
| 2k+2(s-1) |
| 1 |
| 8888 |
解得k=13,s=175.
则这个数记作A(13,175).
故答案为:(13,175)

练习册系列答案
相关题目
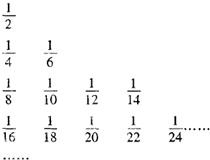 把数列
把数列 把数列{
把数列{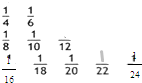 把数列{
把数列{