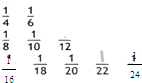
题目内容
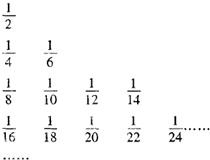 把数列{
把数列{| 1 |
| 2n |
| 1 |
| 4 |
| 1 |
| 2008 |
分析:因为第n行的第一个数为
,先确定则
所在的行数,然后确定列数即可.
| 1 |
| 2n |
| 1 |
| 2008 |
解答:解:因为第n行的第一个数为
,所以当n=10时,
=
,
n=11时,
=
,
所以
位于第10行,由2008=1024+2(m-1),解得m=493,
∴
是第10行的第493个数.
∴
可记为 (10,493).
答案:(10,493)
| 1 |
| 2n |
| 1 |
| 210 |
| 1 |
| 1024 |
n=11时,
| 1 |
| 211 |
| 1 |
| 2048 |
所以
| 1 |
| 2008 |
∴
| 1 |
| 2008 |
∴
| 1 |
| 2008 |
答案:(10,493)
点评:本题考查等比数的性质,难度较大,解题时要认真审题,仔细解答.

练习册系列答案
 长江作业本同步练习册系列答案
长江作业本同步练习册系列答案
相关题目
 把数列{
把数列{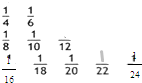 把数列{
把数列{