题目内容
已知函数 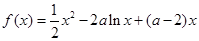 ,
,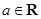 .
.
(1)当 时,求函数
时,求函数 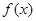 的最小值;
的最小值;
(2)当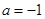 时,求证:无论
时,求证:无论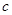 取何值,直线
取何值,直线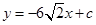 均不可能与函数
均不可能与函数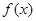 相切;
相切;
(3)是否存在实数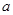 ,对任意的
,对任意的 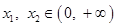 ,且
,且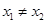 ,有
,有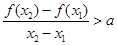 恒成立,若存在求出
恒成立,若存在求出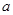 的取值范围,若不存在,说明理由。
的取值范围,若不存在,说明理由。
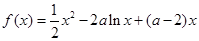 ,
,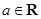 .
.(1)当
 时,求函数
时,求函数 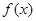 的最小值;
的最小值; (2)当
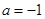 时,求证:无论
时,求证:无论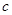 取何值,直线
取何值,直线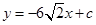 均不可能与函数
均不可能与函数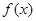 相切;
相切;(3)是否存在实数
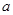 ,对任意的
,对任意的 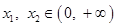 ,且
,且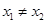 ,有
,有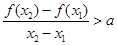 恒成立,若存在求出
恒成立,若存在求出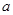 的取值范围,若不存在,说明理由。
的取值范围,若不存在,说明理由。(1)-2ln2;(2)详见解析;(3)存在实数,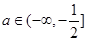 .
.
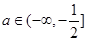 .
.试题分析:(1)把a=1代入函数解析式,求导后得到导函数的零点,由导函数的零点对定义域分段,根据导函数在各区间段内的符号得到原函数的单调性,从而求出函数f(x)的最小值;(2)把a=-1代入原函数,求出导函数后利用基本不等式求出导函数的值域,从而说明无论c 取何值,直线
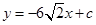 均不可能与函数f(x)相切;(3)假设存在实数a使得对任意的
均不可能与函数f(x)相切;(3)假设存在实数a使得对任意的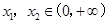 ,且
,且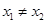 ,有
,有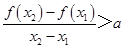 恒成立,假设
恒成立,假设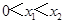 ,则
,则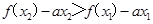 恒成立,构造辅助函数
恒成立,构造辅助函数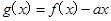 ,只要使函数g(x)在定义域内为增函数即可,利用其导函数恒大于等于0可求解a的取值范围.
,只要使函数g(x)在定义域内为增函数即可,利用其导函数恒大于等于0可求解a的取值范围.解;(1)显然函数
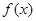 的定义域为
的定义域为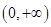 ,
, 当
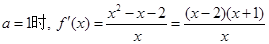 .
.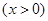
∴ 当
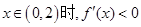 ,
,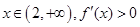 .
.∴
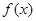 在
在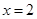 时取得最小值,其最小值为
时取得最小值,其最小值为 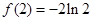 .
.(2)∵
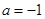
 ,
, 假设直线与
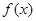 相切,设切点为
相切,设切点为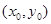 ,则
,则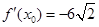
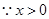
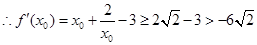 所以
所以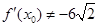 所以无论
所以无论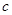 取何值,直线
取何值,直线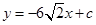 均不可能与函数
均不可能与函数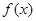 相切。
相切。 (3)假设存在实数
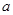 使得对任意的
使得对任意的 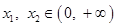 ,且
,且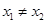 ,有
,有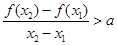 ,恒成立,不妨设
,恒成立,不妨设 ,只要
,只要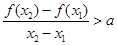 ,即:
,即: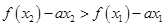
令
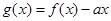 ,只要
,只要 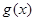 在
在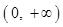 为增函数
为增函数又函数
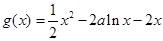 .
.考查函数
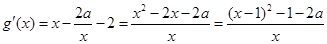
要使
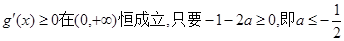 ,
,故存在实数
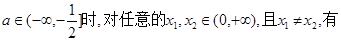
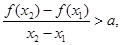 恒成立.
恒成立.
练习册系列答案
相关题目
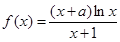 ,曲线
,曲线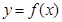 在点
在点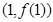 处的切线与直线
处的切线与直线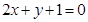 垂直.
垂直.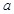 的值;
的值;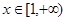 ,
,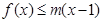 恒成立,求
恒成立,求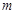 的范围;
的范围;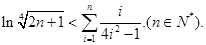
 表示时间,以月为单位,年初为起点,根据历年数据,某水库的蓄水量(单位:亿立方米)关于
表示时间,以月为单位,年初为起点,根据历年数据,某水库的蓄水量(单位:亿立方米)关于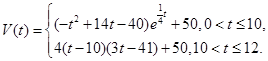
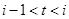 表示第1月份(
表示第1月份( ),同一年内哪几个月份是枯水期?
),同一年内哪几个月份是枯水期?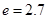 计算).
计算).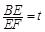 ,EF=l,l关于t的函数为
,EF=l,l关于t的函数为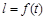 .
. 
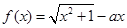
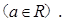
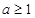 时,函数
时,函数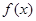 在区间
在区间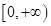 上是单调递减函数;
上是单调递减函数;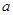 的取值范围,使函数
的取值范围,使函数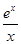 ,f(2)=
,f(2)=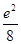 ,则x>0时,f(x)( )
,则x>0时,f(x)( ) 在区间
在区间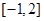 上是减函数,那么
上是减函数,那么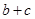 的最大值为 .
的最大值为 .