题目内容
(本小题满分14分)矩形纸片ABCD的边AB=6,AD=10,点E、F分别在边AB和BC上(不含端点). 现将纸片的右下角沿EF翻折,使得顶点B翻折后的新位置B1恰好落在边AD上. 设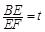 ,EF=l,l关于t的函数为
,EF=l,l关于t的函数为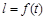 .
.
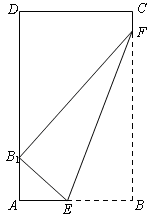
试求:(1)函数f(t)的定义域;
(2)函数f(t)的最小值.
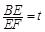 ,EF=l,l关于t的函数为
,EF=l,l关于t的函数为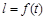 .
. 
试求:(1)函数f(t)的定义域;
(2)函数f(t)的最小值.
(1) (2)
(2)
 (2)
(2)
(1)设
据题意知 为锐角,所以
为锐角,所以 ,从而
,从而 .
.
由于 ,
,
所以
因为 ,且AE+EB=6,
,且AE+EB=6,
所以 ,即
,即
因为F点在BC上,所以 ,即
,即 ,亦即
,亦即 ,
,
所以 ,即
,即 ,解得
,解得 .
.
于是有 ,即
,即 .
.
故函数f(t)的定义域为 8分
8分
(2) 由(1)得
令 ,则由
,则由 ,
, 得:
得:
因此当 时,
时, 单调增,当
单调增,当 时,
时, 单调减.
单调减.
即 时,
时, 取最大值,f(t)取最小值
取最大值,f(t)取最小值 14分
14分
【命题意图】本题考查函数的定义域,值域,二倍角公式,利用导数求函数最值等知识 ,意在考查学生的抽象概括能力,运算求解能力.

据题意知
 为锐角,所以
为锐角,所以 ,从而
,从而 .
. 由于
 ,
,所以

因为
 ,且AE+EB=6,
,且AE+EB=6, 所以
 ,即
,即
因为F点在BC上,所以
 ,即
,即 ,亦即
,亦即 ,
,所以
 ,即
,即 ,解得
,解得 .
. 于是有
 ,即
,即 .
.故函数f(t)的定义域为
 8分
8分(2) 由(1)得

令
 ,则由
,则由 ,
, 得:
得:
因此当
 时,
时, 单调增,当
单调增,当 时,
时, 单调减.
单调减. 即
 时,
时, 取最大值,f(t)取最小值
取最大值,f(t)取最小值 14分
14分【命题意图】本题考查函数的定义域,值域,二倍角公式,利用导数求函数最值等知识 ,意在考查学生的抽象概括能力,运算求解能力.

练习册系列答案
 发散思维新课堂系列答案
发散思维新课堂系列答案
相关题目
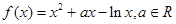 .
.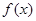 的单调区间;
的单调区间;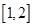 上是减函数,求实数a的取值范围;
上是减函数,求实数a的取值范围;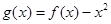 ,是否存在实数a,当
,是否存在实数a,当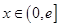 (e是自然对数的底数)时,函数g(x)最小值是3,若存在,求出a的值;若不存在,说明理由.
(e是自然对数的底数)时,函数g(x)最小值是3,若存在,求出a的值;若不存在,说明理由.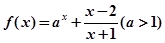
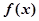 在
在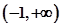 上是增函数;
上是增函数;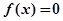 没有负数根.
没有负数根.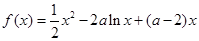 ,
,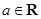 .
. 时,求函数
时,求函数 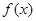 的最小值;
的最小值; 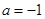 时,求证:无论
时,求证:无论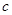 取何值,直线
取何值,直线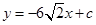 均不可能与函数
均不可能与函数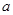 ,对任意的
,对任意的 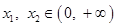 ,且
,且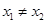 ,有
,有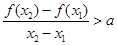 恒成立,若存在求出
恒成立,若存在求出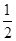 .
.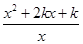 ,对?x1∈(0,+∞),?x2∈(-∞,0)使得f(x1)≤g(x2)成立,求正实数k的取值范围;
,对?x1∈(0,+∞),?x2∈(-∞,0)使得f(x1)≤g(x2)成立,求正实数k的取值范围;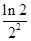 +
+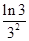 +…+
+…+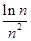 <
<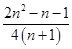 (n∈N*,n≥2).
(n∈N*,n≥2).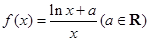 .
.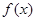 的单调区间和极值;
的单调区间和极值;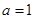 ,且
,且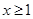 时,证明:
时,证明: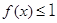 .
.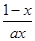 +lnx,若函数f(x)在[1,+∞)上为增函数,则正实数a的取值范围为________.
+lnx,若函数f(x)在[1,+∞)上为增函数,则正实数a的取值范围为________. 的导函数
的导函数 的图像如图所示,则( )
的图像如图所示,则( )
 为
为 为
为 为
为 为
为 ax3+(a-2)x+c的图象如图所示.
ax3+(a-2)x+c的图象如图所示.
 -2ln x在其定义域内为增函数,求实数k的取值范围.
-2ln x在其定义域内为增函数,求实数k的取值范围.