题目内容
设函数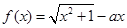
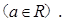
求证:当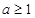 时,函数
时,函数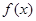 在区间
在区间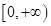 上是单调递减函数;
上是单调递减函数;
求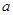 的取值范围,使函数
的取值范围,使函数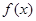 在区间
在区间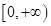 上是单调函数.
上是单调函数.
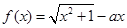
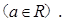
求证:当
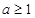 时,函数
时,函数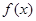 在区间
在区间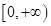 上是单调递减函数;
上是单调递减函数;求
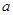 的取值范围,使函数
的取值范围,使函数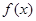 在区间
在区间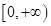 上是单调函数.
上是单调函数.(1)当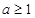 时,函数
时,函数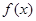 在区间
在区间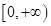 上是单调递减函数.
上是单调递减函数.
(2)当 或
或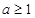 时,函数
时,函数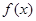 在区间
在区间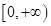 上是单调函数
上是单调函数
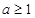 时,函数
时,函数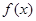 在区间
在区间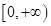 上是单调递减函数.
上是单调递减函数.(2)当
 或
或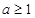 时,函数
时,函数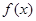 在区间
在区间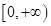 上是单调函数
上是单调函数解:



(1)
 当
当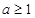 时,
时,
 当
当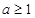 时,函数
时,函数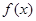 在区间
在区间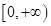 上是单调递减函数.
上是单调递减函数.(2)

 当
当 时,
时, ;当
;当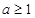 时,
时, . (11分)
. (11分)因此,当
 或
或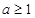 时,函数
时,函数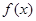 在区间
在区间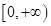 上是单调函数
上是单调函数
练习册系列答案
相关题目
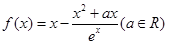 .
. 时,证明:当
时,证明:当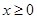 时,
时,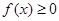 ;
;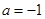 时,证明:
时,证明: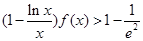 .
. +alnx(x>0).
+alnx(x>0). [f(x1)+f(x2)]≥f
[f(x1)+f(x2)]≥f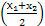 成立,则称函数y=f(x)为区间D上的“凹函数”.试证当a≤0时,f(x)为“凹函数”.
成立,则称函数y=f(x)为区间D上的“凹函数”.试证当a≤0时,f(x)为“凹函数”.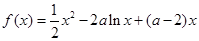 ,
,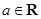 .
. 时,求函数
时,求函数 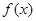 的最小值;
的最小值; 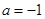 时,求证:无论
时,求证:无论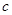 取何值,直线
取何值,直线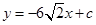 均不可能与函数
均不可能与函数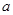 ,对任意的
,对任意的 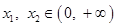 ,且
,且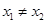 ,有
,有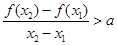 恒成立,若存在求出
恒成立,若存在求出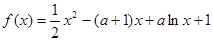
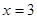 是
是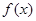 的极值点,求
的极值点,求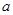 的范围,使得
的范围,使得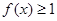 恒成立.
恒成立.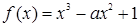 在
在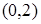 上单调递减,则实数
上单调递减,则实数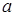 的取值范围为( )
的取值范围为( )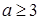
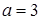
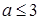
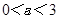
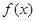 是定义在R上的奇函数,且
是定义在R上的奇函数,且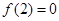 ,当x>0时,有
,当x>0时,有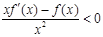 恒成立,则不等式
恒成立,则不等式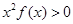 的解集是 ( )
的解集是 ( )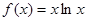 ,当
,当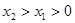 时,给出下列几个结论:
时,给出下列几个结论: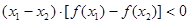 ;②
;②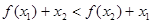 ;③
;③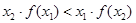 ;
;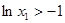 时,
时,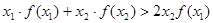 .
.