��Ŀ����
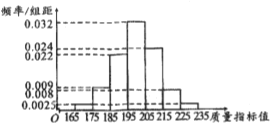
����Ŀ��ʮ������ĩ������ѧ�߱��������о����θ���ʱ����ˡ���������ۡ���������һ��Բ������ѡһ���ң������ҵ��ҳ��������Բ���ڽӵȱ������α߳��ĸ����Ƕ��٣����������á�����뾶����������˵㡱��������е㡱������������ⷽ���������������ͬ������۵�ìͷֱ�����ʸ������ǿ�ҵش̼��˸����ۻ������ϸ���֪������˵㡱�ķ������£���AΪԲO��һ�����㣬��Բ�������ȡһ��B������AB�������ҳ�AB����ԲO���ڽӵȱ������α߳��ĸ��ʣ����ɡ�����˵㡱������õĸ���Ϊ��������
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
���𰸡�C
��������
�����⻭��ͼ�Σ��������������![]() ��λ�ã����ɲ�ȱ��ǻ����ȵô𰸣�
��λ�ã����ɲ�ȱ��ǻ����ȵô𰸣�
�⣺�衰��![]() �ij�����Բ�ڽ��������α߳���Ϊ�¼�
�ij�����Բ�ڽ��������α߳���Ϊ�¼�![]() ��
��
�Ե�![]() Ϊһ���㣬��Բ����һԲ�ڽ���������
Ϊһ���㣬��Բ����һԲ�ڽ���������![]() ��
��

��Ҫ���������![]() ֻ�������ӻ�
ֻ�������ӻ�![]() �ϣ���Բ�ڽ���������
�ϣ���Բ�ڽ���������![]() ǡ�ý�Բ��3�ȷ֣�
ǡ�ý�Բ��3�ȷ֣�
��![]()
��ѡ��C��

��ϰ��ϵ�д�
�����Ŀ