题目内容
(1)在半径为1的圆的一条直径上任取一点，过该点作垂直于直径的弦，其长度超过该圆内接正三角形的边长
的概率是多少？
(2)在半径为1的圆内任取一点，以该点为中点作弦，问其长超过该圆内接正三角形的边长的概率是多少？
(3)在半径为1的圆周上任取两点，连成一条弦，其长超过该圆内接正三角形边长的概率是多少？
(1)设事件A＝“弦长超过”，弦长只与它跟圆心的距离有关，
∵弦垂直于直径，∴当且仅当它与圆心的距离小于
时才能满足条件，由几何概率公式知P(A)＝.
(2)设事件B＝“弦长超过”，弦被其中点惟一确定，当且仅当其中点在半径为的同心圆内时，才能满足
条件，由几何概率公式知P(B)＝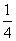
.
(3)设事件C＝“弦长超过”，固定一点A于圆周上，以此点为顶点作内接正三角形ABC，显然只有当弦的另一端点D落在
上时，才有|AD|>|AB|＝，由几何概率公式知P(C)＝
.
练习册系列答案
相关题目
