题目内容
已知点
，
是椭圆
：
上不同的两点，线段
的中点为
.
（1）求直线的方程；
（2）若线段的垂直平分线与椭圆交于点
、
，试问四点
、
、、是否在同一个圆
上，若是，求出该圆的方程；若不是，请说明理由.
解一：（1）
点
，
是椭圆
上不同的两点，
∴
，
.
以上两式相减得：
，
即
，
，
∵线段
的中点为
，
∴
.
∴
，
当
，由上式知，
则
重合，与已知矛盾，因此
，
∴
.
∴直线的方程为
，即
.
由
消去
，得
，解得
或
.
∴所求直线的方程为.
解二: 当直线的不存在时, 的中点在
轴上, 不符合题意.
故可设直线的方程为
, 
.
由
消去，得
(*)
.
的中点为
,
.
.
解得
.
此时方程(*)为,其判别式
.
∴所求直线的方程为.
（2）由于直线的方程为，
则线段的垂直平分线
的方程为
，即
.
由
得
，
由
消去得
，设
则
.
∴线段的中点
的横坐标为
，纵坐标
.
∴
.
∴
.
∵
，
，
∴四点
、
、
、
在同一个圆上，此圆的圆心为点，半径为
，
. 
阅读快车系列答案
（2012•枣庄一模）已知椭圆C1：
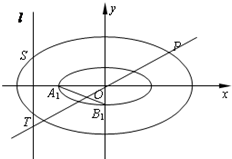如图，椭圆C1与椭圆C2中心在原点，焦点均在x轴上，且离心率相同．椭圆C1的长轴长为
、
分别是椭圆C: 
的左焦点和右焦点,O是坐标系原点, 且椭圆C的焦距为6, 过
两端点
与
的周长是
.
，
是椭圆C上不同的两点，线段
的中点为
.
、
，试问四点
、
、