题目内容
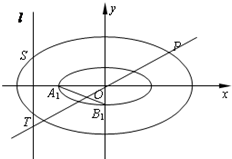 如图,椭圆C1与椭圆C2中心在原点,焦点均在x轴上,且离心率相同.椭圆C1的长轴长为2
如图,椭圆C1与椭圆C2中心在原点,焦点均在x轴上,且离心率相同.椭圆C1的长轴长为2| 2 |
| 3 |
(1)求椭圆C1与椭圆C2的方程;
(2)设点A1为椭圆C1的左顶点,点B1为椭圆C1的下顶点,若直线OP刚好平分A1B1,求点P的坐标;
(3)若点M,N在椭圆C1上,点P,M,N满足
| OP |
| OM |
| ON |
分析:(1)设椭圆C1方程为
+
=1(a1>b1>0),椭圆C2方程为
+
=1(a2>b2>0),由于2a1=2
,可得a1=
,又其左准线x=-2=-
,可得c1=1,则b1=
.可得椭圆C1的离心率为e1=
.
由于两个椭圆的离心率相同可得:椭圆C2中
=2
,由线段的ST长为2
,得S(-2,
),代入椭圆C2的方程得可得
,即可得到
.
(2)利用中点坐标公式可得线段A1B1的中点坐标,进而得到直线OP的方程,与椭圆的方程联立即可得到点P的坐标;
(3)设P(x0,y0),M(x1,y1),N(x2,y2),则
+2
=10,
+2
=2,
+2
=2,由
=
+2
可得:(x0,y0)=(x1,y1)+2(x2,y2),利用向量相等可得
于是
+2
=(x1+2x2)2+2(y1+2y2)2=10,展开即可得出x1x2+2y1y2=0,进而得到kOM•kON为定值.
| x2 | ||
|
| y2 | ||
|
| x2 | ||
|
| y2 | ||
|
| 2 |
| 2 |
| ||
| c1 |
|
| ||
| 2 |
由于两个椭圆的离心率相同可得:椭圆C2中
| a | 2 2 |
| b | 2 2 |
| 3 |
| 3 |
| b | 2 2 |
| a | 2 2 |
(2)利用中点坐标公式可得线段A1B1的中点坐标,进而得到直线OP的方程,与椭圆的方程联立即可得到点P的坐标;
(3)设P(x0,y0),M(x1,y1),N(x2,y2),则
| x | 2 0 |
| y | 2 0 |
| x | 2 1 |
| y | 2 1 |
| x | 2 2 |
| y | 2 2 |
| OP |
| OM |
| ON |
|
| x | 2 0 |
| y | 2 0 |
解答:解:(1)设椭圆C1方程为
+
=1(a1>b1>0),椭圆C2方程为
+
=1(a2>b2>0),
则2a1=2
,∴a1=
,又其左准线x=-2=-
,
∴c1=1,则b1=1
∴椭圆C1方程为
+y2=1,其离心率为e1=
,
∴椭圆C2中
=2
,
由线段的ST长为2
,得S(-2,
),代入椭圆C2
+
=1,得
=5,
∴
=10,
∴椭圆C2方程为
+
=1;
(2)A1(-
,0),B1(0,-1),
则A1B1中点为(-
,-
),
∴直线OP为y=
x,
由
,得
或
,
∴点P的坐标为(
,
),(-
,-
);
(3)设P(x0,y0),M(x1,y1),N(x2,y2),
则
+2
=10,
+2
=2,
+2
=2,
由
=
+2
可得:(x0,y0)=(x1,y1)+2(x2,y2),
∴
∴
+2
=(x1+2x2)2+2(y1+2y2)2
=
+4x1x2+4
+2
+8y1y2+8
=(
+2
)+4(
+2
)+6(x1x2+2y1y2)=10+6(x1x2+2y1y2)=10
∴x1x2+2y1y2=0,
∴
=-
,即kOM•kON=-
,
∴直线OM与直线ON的斜率之积为定值,且定值为-
.
| x2 | ||
|
| y2 | ||
|
| x2 | ||
|
| y2 | ||
|
则2a1=2
| 2 |
| 2 |
| ||
| c1 |
∴c1=1,则b1=1
∴椭圆C1方程为
| x2 |
| 2 |
| ||
| 2 |
∴椭圆C2中
| a | 2 2 |
| b | 2 2 |
由线段的ST长为2
| 3 |
| 3 |
| 4 | ||
2
|
| 3 | ||
|
| b | 2 2 |
∴
| a | 2 2 |
∴椭圆C2方程为
| x2 |
| 10 |
| y2 |
| 5 |
(2)A1(-
| 2 |
则A1B1中点为(-
| ||
| 2 |
| 1 |
| 2 |
∴直线OP为y=
| ||
| 2 |
由
|
|
|
∴点P的坐标为(
| 5 |
| ||
| 2 |
| 5 |
| ||
| 2 |
(3)设P(x0,y0),M(x1,y1),N(x2,y2),
则
| x | 2 0 |
| y | 2 0 |
| x | 2 1 |
| y | 2 1 |
| x | 2 2 |
| y | 2 2 |
由
| OP |
| OM |
| ON |
∴
|
∴
| x | 2 0 |
| y | 2 0 |
=
| x | 2 1 |
| x | 2 2 |
| y | 2 1 |
| y | 2 2 |
=(
| x | 2 1 |
| y | 2 1 |
| x | 2 2 |
| y | 2 2 |
∴x1x2+2y1y2=0,
∴
| y1y2 |
| x1x2 |
| 1 |
| 2 |
| 1 |
| 2 |
∴直线OM与直线ON的斜率之积为定值,且定值为-
| 1 |
| 2 |
点评:本题考查了椭圆的标准方程及其性质、直线与椭圆相交问题转化为方程联立、向量相等、斜率计算公式、整体代入等基础知识与基本技能方法,考查了推理能力和计算能力,属于难题.

练习册系列答案
 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案 综合自测系列答案
综合自测系列答案
相关题目
 如图,椭圆C1:
如图,椭圆C1: (2013•海口二模)定义:若两个椭圆的离心率相等,则称两个椭圆是“相似”的. 如图,椭圆C1与椭圆C2是相似的两个椭圆,并且相交于上下两个顶点.椭圆C1:
(2013•海口二模)定义:若两个椭圆的离心率相等,则称两个椭圆是“相似”的. 如图,椭圆C1与椭圆C2是相似的两个椭圆,并且相交于上下两个顶点.椭圆C1: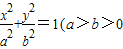 ,a,b为常数),动圆
,a,b为常数),动圆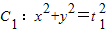 ,b<t1<a.点A1,A2分别为C的左,右顶点,C1与C相交于A,B,C,D四点.
,b<t1<a.点A1,A2分别为C的左,右顶点,C1与C相交于A,B,C,D四点. 与C相交A′,B′,C′,D′四点,其中b<t2<a,t1≠t2.若矩形ABCD与矩形A′B′C′D′的面积相等,证明:
与C相交A′,B′,C′,D′四点,其中b<t2<a,t1≠t2.若矩形ABCD与矩形A′B′C′D′的面积相等,证明: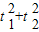 为定值.
为定值.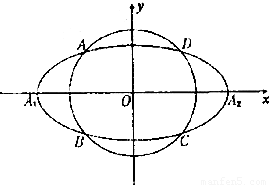
 ,a,b为常数),动圆
,a,b为常数),动圆 ,b<t1<a.点A1,A2分别为C的左,右顶点,C1与C相交于A,B,C,D四点.
,b<t1<a.点A1,A2分别为C的左,右顶点,C1与C相交于A,B,C,D四点. 与C相交A′,B′,C′,D′四点,其中b<t2<a,t1≠t2.若矩形ABCD与矩形A′B′C′D′的面积相等,证明:
与C相交A′,B′,C′,D′四点,其中b<t2<a,t1≠t2.若矩形ABCD与矩形A′B′C′D′的面积相等,证明: 为定值.
为定值.