题目内容
已知直线l的参数方程为
(t为参数),曲线C的极坐标方程为ρ=4cosθ,则直线l被曲线C截得的弦长为 .
|
考点:直线的参数方程
专题:计算题,坐标系和参数方程
分析:先将极坐标方程两边同乘以ρ后化成直角坐标方程,将直线l的参数方程化成普通方程,再求直线l被曲线C截得的弦长.
解答:
解:曲线C的极坐标方程为ρ=4cosθ,直角坐标方程是:x2+y2-4x=0,
直线l的普通方程是:y=
x-
,
联立解方程组,得4x2-10x+3=0,
设交点坐标为(x1,y1),(x2,y2),则直线l被曲线C截得的弦长为
•
=
.
故答案为:
.
直线l的普通方程是:y=
| 3 |
| 3 |
联立解方程组,得4x2-10x+3=0,
设交点坐标为(x1,y1),(x2,y2),则直线l被曲线C截得的弦长为
| 1+3 |
(
|
| 13 |
故答案为:
| 13 |
点评:本题主要考查了简单曲线的极坐标方程,以及直线的参数方程等知识,属于基础题.

练习册系列答案
 学练快车道快乐假期寒假作业系列答案
学练快车道快乐假期寒假作业系列答案
相关题目
在一次运动会上有四项比赛的冠军在甲、乙、丙三人中产生,那么不同的夺冠情况共有( )种.
A、A
| ||
| B、43 | ||
| C、34 | ||
D、C
|
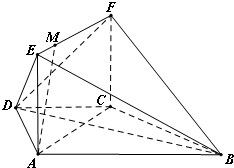 如图,在梯形ABCD中,AD⊥CD,AB∥CD,AD=CD=
如图,在梯形ABCD中,AD⊥CD,AB∥CD,AD=CD=