题目内容
15.某货运员拟运送甲、乙两种货物,每件货物的体积、重量、可获利润以及运输限制如表:| 货物 | 体积(升/件) | 重量(公斤/件) | 利润(元/件) |
| 甲 | 20 | 10 | 8 |
| 乙 | 10 | 20 | 10 |
| 运输限制 | 110 | 100 |
分析 运送甲x件,乙y件,利润为z,建立约束条件和目标函数,利用线性规划的知识进行求解即可.
解答 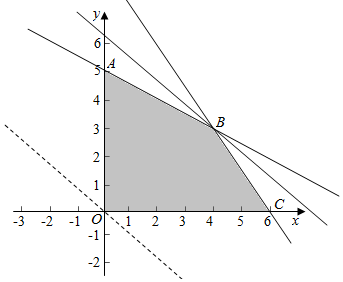 解:设运送甲x件,乙y件,利润为z,
解:设运送甲x件,乙y件,利润为z,
则由题意得$\left\{\begin{array}{l}{20x+10y≤110}\\{10x+20y≤100}\\{x,y∈N}\end{array}\right.$,即$\left\{\begin{array}{l}{2x+y≤11}\\{x+2y≤10}\\{x,y∈N}\end{array}\right.$,且z=8x+10y
作出不等式组对应的平面区域如图:
由z=8x+10y得y=-$\frac{4}{5}$x+$\frac{z}{10}$,
平移直线y=-$\frac{4}{5}$x+$\frac{z}{10}$,由图象知当直线y=-$\frac{4}{5}$x+$\frac{z}{10}$经过点B时,直线的截距最大,此时z最大,
由$\left\{\begin{array}{l}{2x+y=11}\\{x+2y=10}\end{array}\right.$,得$\left\{\begin{array}{l}{x=4}\\{y=3}\end{array}\right.$,即B(4,3),
此时z=8×4+10×3=32+30=62,
故答案为:62
点评 本题主要考查线性规划的应用,设出变量,建立约束条件和目标函数,作出图象,利用线性规划的知识进行求解是解决本题的关键.

练习册系列答案
相关题目
5.已知奇函数F(x)=$\left\{\begin{array}{l}{(\frac{1}{2})^{x}-\frac{4}{3},(x>0)}\\{f(x),(x<0)}\end{array}\right.$,则F(f(log2$\frac{1}{3}$))=( )
| A. | -$\frac{5}{6}$ | B. | $\frac{5}{6}$ | C. | ($\frac{1}{2}$)${\;}^{\frac{13}{3}}$ | D. | ($\frac{1}{2}$)${\;}^{\frac{1}{3}}$-$\frac{4}{3}$ |
6.有三个房间需要粉刷,粉刷方案要求:每个房间只用一种颜色,且三个房间颜色各不相同.三个房间的粉刷面积和三种颜色的涂料费用如表:
那么在所有不同的粉刷方案中,最低的涂料总费用是1464元.
| 房间A | 房间B | 房间C |
| 35m2 | 20m2 | 28m2 |
| 涂料1 | 涂料2 | 涂料3 |
| 16元/m2 | 18元/m2 | 20元/m2 |
3.如图是计算$\frac{1}{2}+\frac{1}{4}+\frac{1}{8}+…+\frac{1}{512}$的值的一个程序框图,其中判断框内可以填的是( )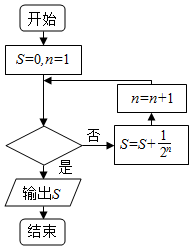

| A. | n≥12? | B. | n≥11? | C. | n≥10? | D. | n≥9? |
10. 执行如图所示的程序框图,若输入的M的值为55,则输出的i的值为( )
执行如图所示的程序框图,若输入的M的值为55,则输出的i的值为( )
 执行如图所示的程序框图,若输入的M的值为55,则输出的i的值为( )
执行如图所示的程序框图,若输入的M的值为55,则输出的i的值为( )| A. | 3 | B. | 4 | C. | 5 | D. | 6 |
4.执行如图所示的程序框图,输出c的结果为( )
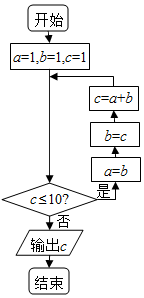

| A. | 13 | B. | 21 | C. | 17 | D. | 15 |
