题目内容
设各项均为正数的数列
的前
项和为
，满足
，
，且
、
、
构成等比数列．
（1）证明:
；（2）求数列的通项公式；
（3）证明:对一切正整数，有
．
【解析】（1）在中令
，
可得
，而
，∴．
（2）由可得
(
)．
两式相减，可得
，即
，
∵
，∴
，
于是数列把第1项去掉后，是公差为2的等差数列．
由、、成等比数列可得
，
即
，解得
，
由可得
，于是
，
∴数列是首项为1，公差为2的等差数列，
∴
．
（3）∵
，
∴
．
练习册系列答案
三新快车金牌周周练系列答案
相关题目
．
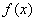的奇偶性；
上是增函数，求实数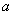
的取值范围.
满足
，求
.
的各项均为正数，且
，则
.
中, 
，则它的前9项和
（ ）
B.
C.
D.
中，
，求
满足
.
；(2)令
,求数列
的前
项和
.
是数列
的前
项和，且
，当
时，有
．(1)求证：
是等比数列；(2)求数列