题目内容
【题目】已知等差数列
的前n项和为
，
，公差为
若
，求数列的通项公式；
是否存在d，n使
成立？若存在，试找出所有满足条件的d，n的值，并求出数列的通项公式；若不存在，请说明理由．
【答案】（1）
；（2）见解析
【解析】
由已知求得公差，直接代入等差数列的通项公式得答案；
由
，得到
，然后依次取n值，求得d，分类分析即可得到所有满足条件的d，n的值，并求得通项公式．
当
时，由
，得
，即
．
；
由题意可知，
，
即
，
．
令
时，得
，不合题意；
时，得
，符合．
此时数列的通项公式为
；
时，得
，不合题意；
时，得
，符合．
此时数列的通项公式为
；
时，得
，符合．
此时数列的通项公式为
；
时，得
，不合题意；
时，得
，不合题意；
时，得
，不合题意；
时，
，均不合题意．
存在3组，其解与相应的通项公式分别为：
，，；
，，；
，，．
练习册系列答案
相关题目
【题目】某品牌手机厂商推出新款的旗舰机型，并在某地区跟踪调查得到这款手机上市时间（第
周）和市场占有率（
）的几组相关数据如下表：
|
|
|
|
|
|
|
|
|
|
|
|
（1）根据表中的数据，用最小二乘法求出
关于的线性回归方程
；
（2）根据上述线性回归方程，预测在第几周，该款旗舰机型市场占有率将首次超过
（最后结果精确到整数）．
参考公式：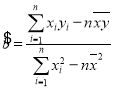
，
．
