题目内容
【题目】(1)当![]() 时,不等式
时,不等式![]() 恒成立,求实数
恒成立,求实数![]() 的取值范围;
的取值范围;
(2)已知函数![]() ,
,![]() ,如果函数
,如果函数![]() 有两个极值点
有两个极值点![]() 、
、![]() ,求证:
,求证:![]() .(参考数据:
.(参考数据:![]() ,
,![]() ,
,![]() ,
,![]() 为自然对数的底数)
为自然对数的底数)
【答案】(1)![]() ;(2)证明见解析.
;(2)证明见解析.
【解析】
(1)构造函数![]() ,其中
,其中![]() ,可得
,可得![]() ,求出函数
,求出函数![]() 的导数
的导数 ,构造函数
,构造函数![]() ,分
,分![]() 和
和![]() 两种情况讨论,结合
两种情况讨论,结合![]() 可求出实数
可求出实数![]() 的取值范围;
的取值范围;
(2)由题意得出 ,变形得
,变形得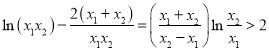 ,利用基本不等式得出
,利用基本不等式得出![]() ,然后构造函数
,然后构造函数![]() ,利用导数分析函数
,利用导数分析函数![]() 的单调性,证明出
的单调性,证明出![]() ,结合单调性可得出
,结合单调性可得出![]() .
.
(1)令![]() ,其中
,其中![]() ,且有
,且有![]() ,
,
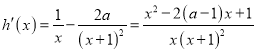 ,
,
令![]() ,则
,则![]() .
.
①当![]() 时,即当
时,即当![]() 时,对任意的
时,对任意的![]() ,
,![]() ,即
,即![]() ,
,
所以,函数![]() 在区间
在区间![]() 上为增函数,当
上为增函数,当![]() 时,
时,![]() ,合乎题意;
,合乎题意;
②当![]() 时,则
时,则![]() 或
或![]() .
.
(i)当![]() 时,对任意的
时,对任意的![]() ,
,![]() ,即
,即![]() ,
,
所以,函数![]() 在区间
在区间![]() 上为增函数,当
上为增函数,当![]() 时,
时,![]() ,合乎题意;
,合乎题意;
(ii)当![]() 时,设函数
时,设函数![]() 的两个极值点分别为
的两个极值点分别为![]() 、
、![]() ,设
,设![]() ,
,
由韦达定理得 ,则必有
,则必有![]() ,
,
当![]() 时,
时,![]() ,当
,当![]() 时,
时,![]() .
.
所以,![]() ,不合乎题意.
,不合乎题意.
综上所述,实数![]() 的取值范围是
的取值范围是![]() ;
;
(2)若![]() ,
,
则![]() 有两个不同的零点
有两个不同的零点![]() 、
、![]() .
.
由题意 ,相加有
,相加有![]() ,①
,①
相减有 ,从而
,从而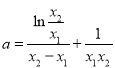 ,
,
代入①有 ,
,
即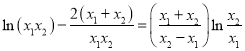 ,
,
不妨设![]() ,则
,则![]() ,由(1)有
,由(1)有![]()
 .
.
又![]()
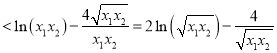 ,
,
所以![]() ,即
,即![]() ,
,
设![]() ,则
,则![]() ,
,![]() 在
在![]() 单调递增,
单调递增,
又![]() ,
,
![]() ,
,![]() ,因此
,因此![]() .
.

【题目】世界卫生组织的最新研究报告显示,目前中国近视患者人数多达6亿,高中生和大学生的近视率均已超过七成,为了研究每周累计户外暴露时间(单位:小时)与近视发病率的关系,对某中学一年级200名学生进行不记名问卷调查,得到如下数据:
每周累积户外暴露时间(单位:小时) |
|
|
|
| 不少于28小时 |
近视人数 | 21 | 39 | 37 | 2 | 1 |
不近视人数 | 3 | 37 | 52 | 5 | 3 |
(1)在每周累计户外暴露时间不少于28小时的4名学生中,随机抽取2名,求其中恰有一名学生不近视的概率;
(2)若每周累计户外暴露时间少于14个小时被认证为“不足够的户外暴露时间”,根据以上数据完成如下列联表,并根据(2)中的列联表判断能否在犯错误的概率不超过0.01的前提下认为不足够的户外暴露时间与近视有关系?
近视 | 不近视 | |
足够的户外暴露时间 | ||
不足够的户外暴露时间 |
附:![]()
P | 0.050 | 0.010 | 0.001 |
| 3.841 | 6.635 | 10.828 |