题目内容
设同时满足条件:①![]() ≤bn+1(n∈N+);②bn≤M(n∈N+,M是与n无关的常数)的无穷数列{bn}叫“特界”数列.
≤bn+1(n∈N+);②bn≤M(n∈N+,M是与n无关的常数)的无穷数列{bn}叫“特界”数列.
(1)若数列{an}为等差数列,Sn是其前n项和,a3=4,S3=18,求Sn;
(2)判断(1)中的数列{Sn}是否为“特界”数列,并说明理由.
(1)设等差数列{an}的公差为d,
则a1+2d=4,S3=a1+a2+a3=3a1+3d=18,
解得a1=8,d=-2,
∴Sn=na1+![]() d=-n2+9n.
d=-n2+9n.
(2)由![]() -Sn+1=
-Sn+1=![]() =
=![]() =
=![]() =-1<0
=-1<0
得![]() <Sn+1,故数列{Sn}适合条
<Sn+1,故数列{Sn}适合条![]() 件①
件①
而Sn=-n2+9n=-(n-![]() )2+
)2+![]() (n∈N+),则当n=4或5时,Sn有最大值20,
(n∈N+),则当n=4或5时,Sn有最大值20,
即Sn≤20,故数列{Sn}适合条件②.
综上,数列{Sn}是![]() “特界”数列.
“特界”数列.

练习册系列答案
相关题目
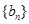 是首项为
是首项为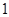 ,公比为
,公比为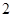 的等比数列.数列
的等比数列.数列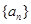 满足
满足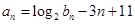 ,
,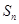 是
是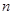 项和.
项和.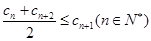 ;②
;② (
(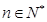 ,
,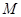 是与
是与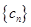 叫“特界”数列.判断(1)中的数列
叫“特界”数列.判断(1)中的数列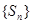 是否为“特界”数列,并说明理由.
是否为“特界”数列,并说明理由.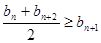 ;②
;②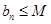 (
( ,
,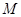 是与
是与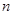 无关的常数)的无穷数列
无关的常数)的无穷数列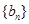 叫“嘉文”数列.已知数列
叫“嘉文”数列.已知数列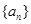 的前
的前 满足:
满足: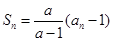 (
(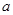 为常数,且
为常数,且 ,
,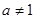 ).
).  ,若数列
,若数列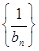 为“嘉文”数列.
为“嘉文”数列.